Kurven erkunden und verstehen, Website zum Buch

11 Elemente der Analysis für Kurven

Website zum Buch: Hier sind die Dateien, die die Bilder des Buches erzeugt haben, die Aufgabenlösungen, Beweis-Ergänzungen und weitere Kurven, für die im Buch kein Platz mehr war. Wenn Sie hier etwas nicht verstehen, lesen Sie im Buch. Falls Sie Fehler finden ober noch Fragen übrig sind, wenden Sie sich an mich.

11.1 Kurven

11.2 Steigung und Ableitung

11.3 Flächen und Rotationsvolumnina

11.4 Bogenlängen

11.5 Krümmungen

11.1 Kurven im Blick der Analysis
Kap: Seite 11: S. 318	Die Analysis ist ein so mächtiges und in Schule und Hochschule auch so wesentliches Werkzeug, dass es auch in diesem Buch zum Tragen kommen soll. Dabei verwende ich eine pragmatische Schreibweise, bei der mit \(\Delta\), dem grossen griechischen Delta, stets kleine Differenzen der darauf folgendeSn Größe bezeichnet werden, \(\Delta r \) ist eine kleine Änderung des Polarradius \( f \), \(\Delta \theta\) eine kleine Winkeldifferenz u. s. w. Das Konzept der Analysis, genauer der Infinitesimalrechnung, ist es, diese kleinen Differenzen durch einen Grenzprozess ad infinitum, zum unendlich Kleinen, zu Differenzialen werden zu lassen. Aus \(\Delta r\) wird dann \(d r\), aus \(\Delta \theta\) wird \(d \theta\) u. s. w. Die hilfreiche und übersichtliche Darstellungsweise wird an anderen Stellen eines Analysislehrganges adressatengemäß abgesichert durch Betrachtung "ordentlicher" Grenzwerte. Die umgekehrte Stoßrichtung, differenzielle Größen zu einer Gesamtheit zusammenzufassen, führt zum Integral - das lateinische integer heist ganz -. So wird z. B. aus \(\Delta A = f(x) \Delta x\), den kleinen rechteckigen Balken beim Riemann'schen Integral, in differenzieller Schreibweise \(d A = f(x) d x\), das infinitesimale Flächenelement. Mit \( A = \int_a^b{f(x)} \; dx \) erhält man die Gesamtheit aller infinitesimalen Balken zwischen \(a\) und \(b\), die ganze Fläche \(A\). Mit dieser Grundidee sollen im Folgenden das Arsenal der fur Kurven wichtigen Analysiswerkzeuge fur die lokalen Begriffe Steigung und Krümmung und die globalen Begriffe Fläche, Rotationsvolumen und Bogenlänge vorgestellt und hergeleitet werden. Entsprechende Formeln stehen natürlich im [Bronstein 1999] und anderen gängigen Formelsammlungen. Ich habe mich aber zu einer zwar knappen, aber schlüssigen und verständlichen Darstellung entschlossen, da es mir - wie im Titel versprochen - um Verstehen geht.

11.2 Steigung und Ableitung
Kap: Seite 11.2.4.2: S. 320		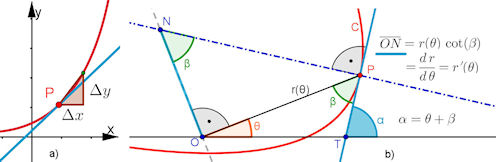Abb. 11.1 Steigung a) Sekantensteigung und Tangente für die explizite kartesische Darstellung, b) Tangente und Normale für Polarkurven
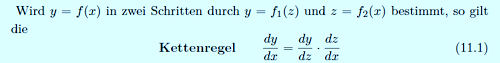
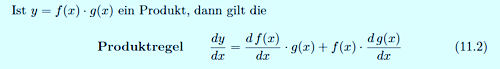
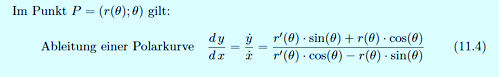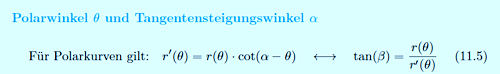
		Sämtliche Herleitungen befinden sich im Buch: Kurven erkunden und verstehen. Link zu "Höhere Mathematik sehen und verstehen". Direkter Link zu der Seite (in neuem Tab), die diesen Abschnitt aufruft: dort Analysis,1.63 Polare Ableitung
11.3 Flächen und Rotationsvolumina
Kap: Seite 11.3.3: S. 323		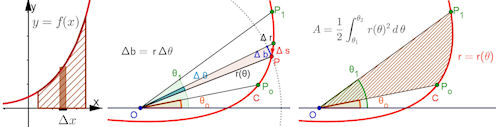Abb. 11.2 Flächen und Kurven: a) Fläche kartesisch, b) Ansatz für Polarkurven: keilförmiges Flächenstuck Delta A, das bei einer WinkeländerungDelta theta entsteht. c) Die Fläche bei Polarkurven ist ein Kurvensektor.

Kap: Seite 11.3.4: S. 324		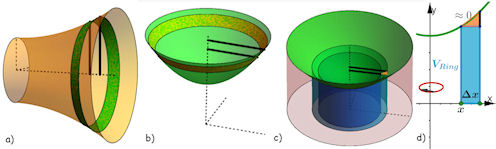Abb. 11.3 Volumina bei Rotation einer Parabel: a) Summation von senkrechten Zylinderscheibchen, b) Summation von waagerechten Zylinderscheibchen, c) Summation von aufrechten Zylinderringen, d) halber Querschnitt des Zylinderringes
		Sämtliche Herleitungen befinden sich im Buch: Kurven erkunden und verstehen.
11.4 Bögenlänge von Kurven
Kap: Seite 11.4.1: S. 325		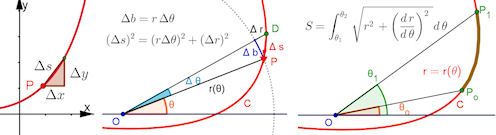Abb. 11.4 Bogenlänge a) für kartesische Funktionen, b) und c) für Polarkurven, Ansatz und Ausführung

11.5 Krümmungen von Kurven
Kap: Seite 11.5.1: S. 327		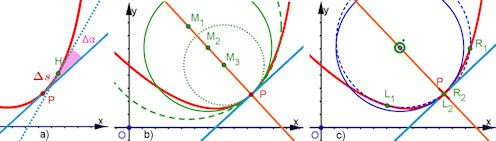Abb. 11.5 a) Krümmung als Grenzwert von (Delta alpha)/(Delta s), b) Krümmungskreis interaktiv mit der Normalen finden, c) Krümmungskreis interaktiv als Kreis durch drei Kurvenpunkte finden (Schupp und Henn)
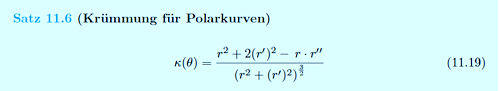
		Sämtliche Herleitungen befinden sich im Buch: Kurven erkunden und verstehen.
Kap: Seite 11.5.4: S. 329		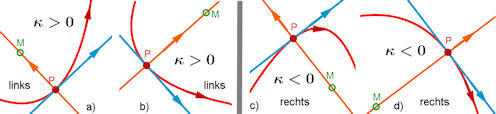Abb. 11.6 Krümmungstypen: a) und b) Linkskrümmung, c) und d) Rechtskrümmung

Für 1/kappa kann man nicht r schreiben, da man das Vorzeichen braucht, aber r stets positiv ist.