|
05 Frei erfunden und hoch hinaus 
5.3 Hoch hinaus in den Raum |
| Website zum Buch: Hier sind die Dateien, die die Bilder des Buches erzeugt haben, die Aufgabenlösungen, Beweis-Ergänzungen und weitere Kurven, für die im Buch kein Platz mehr war. Wenn Sie hier etwas nicht verstehen, lesen Sie im Buch. Falls Sie Fehler finden ober noch Fragen übrig sind, wenden Sie sich an mich. |
| Kap: Seite 5.3.1: S. 148 |
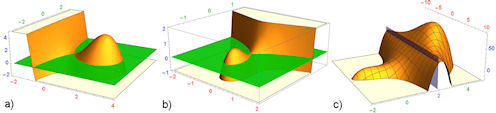 | Abb. 5.11 3D-Familien a) Trisektrix von Maclaurin, b) Konchoide des Nikomedes für kleine z, c) überraschende Form für große z  Strophoide 3D download
| |||
| BBB | |||||
| Kap: Seite 5.3.1: S. 148 |
 
|
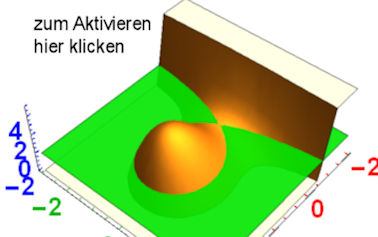Die Raumverwandten der Trisektix ansehen: Interaktiv mit Mathematica  Trisektrix 3D.cdfInfo zum Mathematica-Player
 Mathematica-Notebook dazu
dasselbe lesen und verstehen 
|
|||
| Kap: Seite 5.3.1: S. 148 |
|
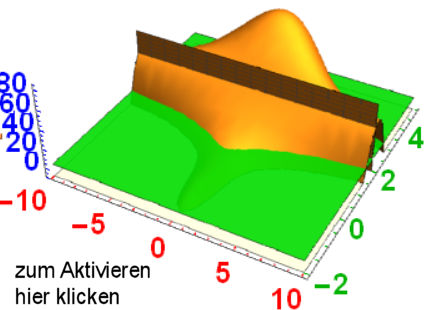Die Raumverwandten der Konchoide der NikomedesKonchoNico3D.cdf
Info zum Mathematica-Player
-->
Mathematica-Notebook dazu
dasselbe lesen und verstehen
| |||
| Kap: Seite 5.3.1: S. 149  5.6 |
 | Raumverwandte Kurven
zu 1.: Neil'sche Parabel 3D download
Zu 2.: Cissoide 3D download
Zu 3.: Strophoide 3D download
Zu 4.: Konchoide 3D download
Zu 4.: Konchoide 3D Ergänzung
| |||
| Kap: Seite 5.3.2.1: S. 150 |
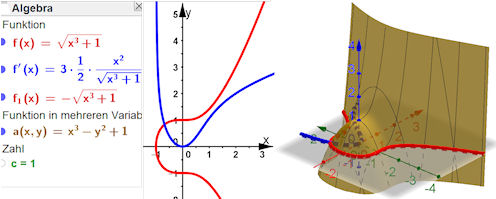
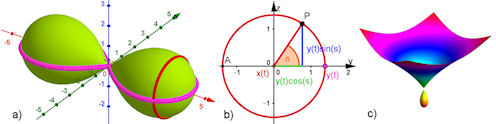 | Abb. 5.12 Rotation von Kurven a) Die Lemniskate rotiert um die x-Achse (GeoGebra), b) Beweiszeichnung zur Erklärung der Formel, c) eine Variante des Newton’schen Knotens Abb. 4.13 d) rotiert um die z-Achse | |||
im GeoGebra-Book
download
Newtonknoten 3D download
| |||||
| Kap: Seite 5.3.2.1: S. 149 |
|
Zu Abb. 5.12 c) Variantes des Newton-Knotens aus Abb. 4.13 d) NewtonKnoten3D.cdf
Info zum Mathematica-Player
Mathematica-Notebook dazu
dasselbe lesen und verstehen
| |||
| Kap: Seite 5.3.2.1: S. 151 |
 | Abb. 5.13 Rotation implizit gegebener Kurven a) Strophoide b) Konchoide des Nikomedes c) erfundene Quartik | |||
| Kap: Seite 5.3.3: S. 152 |
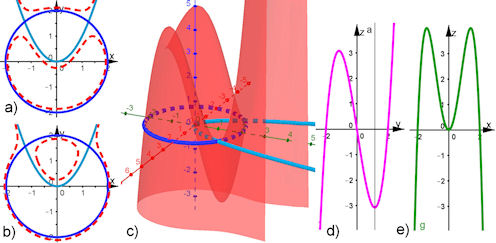 | Abb. 5.14 Produkt implizit gegebener Kurven als Raumfläche a) und b) Kurvenprodukt blau, rot gestrichelt raumverwandte Kurve, oben +1, unten -1, c) Raumfläche d) Schnittkurve mit der y-z-Ebene, e) Schnittkurve mit der x-z-Ebene | |||
| Kap: Seite 5.3.4: S. 154 |
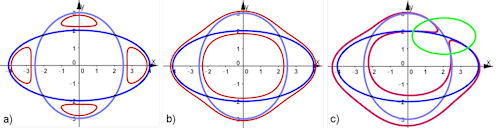 | Abb. 5.15 Produkt von Ellipsen nach Felix Klein und raumverwandte Kurven a) Ellipsen und Schnittkurve mit Ebene h = -0.1, b) entsprechend mit h = +0.1. c) Einbau einer Störung nach Klein und Wieleitner, siehe Abschnitt 5.3.4.2. download
| |||
| Kap: Seite 5.3.4.1: S.154 |
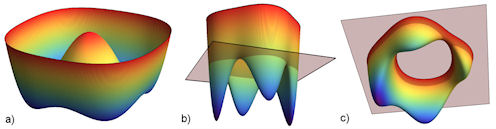
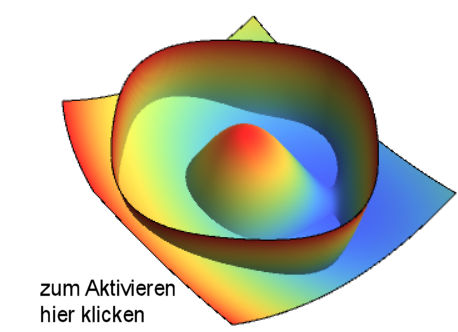| Abb. 5.16 Raumfläche des Produktes von Ellipsen a) im z-Intervall von -0.4 bis 1, b) mit der Grundebene als Ausschnitt, c) mit eingebauter Störung passend zu Abb. 5.15 c) Klein'sche Quartiken KleinQuartiken.cdfInfo zum Mathematica-Player
Mathematica-Notebook dazu
dasselbe lesen und verstehen
|
|||
| Kap. 5.3.5.1 |
| ||||
| Kap: Seite 5.3.5.2: S. 157 |
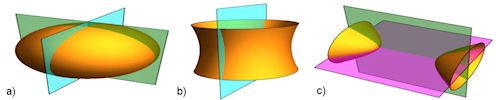 | Abb. 5.17 3D-Quadriken mit drei Quadrattermen a) Ellipsoid, b) einschaliges Hyperboloid, c) zweischaliges Hyperboloid | |||
| Kap: Seite 5.3.5.2: S. 158 |
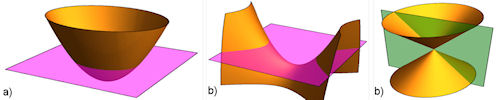 | Abb. 5.18 Weitere Quadriken
a) elliptisches Paraboloid, b) hyperbolisches Paraboloid, c) elliptischer Kegel | |||
| Kap: Seite 5.3.5.2: S. 158 |
 | Abb. 5.19 Quadriken, Parabelrinne, Schnitte a) mit der x-y-Ebene, b) mit der y-z-Ebene, c) mit der x-z-Ebene | |||
| Kap: Seite 5.3.5.2: S. 158 |
 | Abb. 5.20 Zylinder-Quadriken a) elliptischer Zylinder, b) hyperbolischer Zylinder, c) parabolischer Zylinder | |||
5.3.6 Harmonie der rotierten Quadriken | |||||
| Kap: Seite 5.3.6: S. 159 |
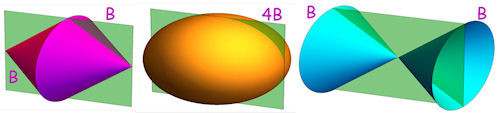 | Abb. 5.21 Kegel und Ellipsoid. B ist der Volumen-Baustein 1/3 pi a b^2, die grüne Fläche hat die Mase 2a x 2b. | |||
| Kap: Seite 5.3.6: S.159 |
 |
Abb. 5.22 Asymptoten-Kegel und Hyperboloid (bis 2a). B ist der Volumen-Baustein 1/3 pi a b^2, Das Ellipsoid nimmt 2/3 des umfassenden Zylinders ein. Es hat dasselbe Volumen wie das Hyperboloid. Dieses halbiert genau seinen Asymptotenkegel. | |||
| Ein Ring der Breite d, irgendwo (ab a) aus dem Zwischenraum zwischen Hyperboloid und Asymptoten-Kegel genommem, ist stets so groß wie eine Scheibe der Dicke d aus dem gezeigten Zylinder. (siehe nachfolgend im Querschnitt) | |||||
| Kap: Seite 5.3.6: S. 160 |
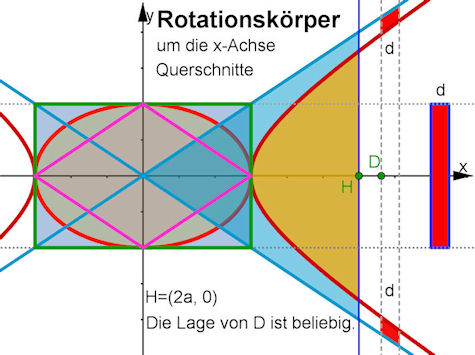 | Abb. 5.23 Querschnitte zu den 3D-Abbildungen
in diesem Abschnitt. Die verwendeten Gleichungen sind z. B. x^2/ a^2 ± y^2/ b^22 = 1 und y = ±b/ a x. Für die 3D-Bilder ist der y^2-Term stets durch einen ebensolchen z^2-Term ergänzt. Für den Zylinder z. B. anstelle von y^2 = b^2 nun y^2+z^2 = b^2. Achten Sie darauf, dass Sie für „Volumen zwischen“ nicht über die Differenz der Ordinaten integrieren dürfen. Parabeln mit dem Scheitel in
O sind hier noch nicht dabei, sie „spielen aber
auch mit“. Lassen sie sich anregen, eigene Ideen
zu verfolgen.
| |||
Exoten | |||||
| Kap: Seite 5.3.7: S. 160 |
 | Abb. 5.24 Exoten a) Rosette mit Wand, b) Lemniskate parametrisch, c) Variante der Lemniskate, parametrisch | |||
| Rosetten-Zylinder Abb. 5.24 a): Mathematica-Befehl: ParametricPlot3D[
{Cos[2 t]Cos[t],Sin[t] Cos[2 t],t z/8},{t,0,2 Pi},{z,0,1}]. In Abwandlung
des Vorgehens bei der impliziten kartesischen 3D-Darstellung, wie sie bei den Zylinder-
Quadriken beschrieben wurde, hat man bei der parametrischen 3D-Darstellung noch die
Möglichkeit, die Wandhöhe des Zylinders zu gestalten. Bei der Rosette mit dem Polarwinkel
t ist in Abb. 5.24 a) die z Koordinate als t z/8
gewählt. Darum wächst die Wand von
Höhe 0 auf die Höhe Pi/4
. Der Startpunkt ist unsichtbar unter der hohen Ecke.
Lemniskaten-Brille Abb. 5.24 b) Der Befehl fur Mathematica ist: ParametricPlot3D[Sin[s] Cos[t] Sqrt[2 e^2 Cos[2 t]], Sin[s] Sin[t] Sqrt[2 e^2 Cos[2 t]], Cos[s] }, {t,0,Pi}, {s,-1,Pi/2}] Optionen fur Farben u. s. w. sind fortgelassen. Lemniskaten-Spiegelschale Abb. 5.24 c) Der Befehl fur Mathematica ist: ParametricPlot3D[Sin[s] Cos[t] Sqrt[2 e^2 Cos[2 t]], Sin[s] Sin[t] Sqrt[2 e^2 Cos[2 t]], Sin[s] }, {t,0,2Pi}, {s,0,3Pi/2}] | |||||
 Prof. Dr. Dörte Haftendorn |
 Erstellt August 2016, Update |
www.kurven-erkunden-und-verstehen.de |
| ||
statt 