6.1 Unlösbarkeit

6.2 Winkel teilen

6.3 Würfel vedoppeln

6.4 n-Ecke konstruieren

6.5 Kreis quadrieren

6.6 Quasi-konstruktionen

6.7 Parabel-Quadratur

6. 1 Die Unlösbarkeit allein mit Zirkel und Lineal
Kap: Seite 6: S. 161
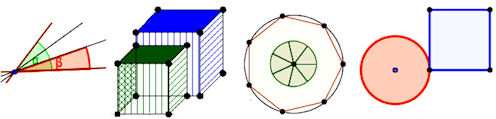	Abb. 6.1 Unlösbeare Probleme    a) Winkel dritteln,    b) Würfel verdoppeln,     c) 7-Eck konstruieren,     d) Kreis quadrieren
Kap: Seite 6.1.2.1: S. 163		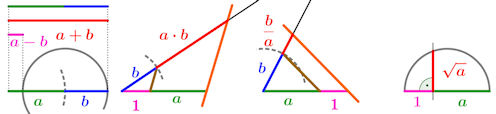Abb. 6.2 Mit Zirkel und Lineal kann man mit Strecken a und b die arithmetischen Operationen a + b, a - b, a mal b, b/a, Wurzel(a) durchführen. Im Buch wird dieses Thema mit Sorgfalt ausgeführt.
	Hauptgedanke für die Unlösbarkeit der oben genannten Probleme ist die Tatsache, dass Schnitte von Kreisen und Geraden nur Quadratwurzel-Schachtelungen erzeugen können, da die Gleichungen höchsten Grad 2 haben. Damit können dritte Wurzeln und vieles mehr mit Zirkel und Lineal nicht konstruiert werden. Dass man nicht doch irgendwie dritte Wurzeln umwandeln kann, folgt aus der "Galoistheorie", auf die das Buch in -möglichst- elementarer Weise eingeht.
6.2 Beliebige Winkel in n Teile teilen
Kap: Seite 6.2: S. 166		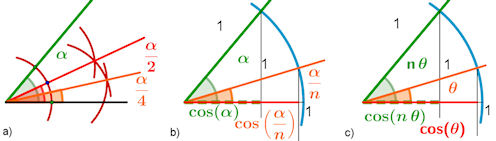Abb. 6.3 Winkelteilen: a) Halbieren, Vierteln, u. s. w. allein mit Zirkel und Lineal, b) und c): zu jedem Winkel (< 180°) gehört eineindeutig sein Kosinus im Einheitskreis, b) alpha und damit cos(alpha) sind gegeben, cos(alpha/n) und letztlich alpha/n sind gesucht, c) bequemer ist: n �theta und damit cos(�n theta) sind gegeben, cos(theta) und letztlich theta sind gesucht. Für x=cos(theta) wird im Buch eine Gleichung 3. Grades hergeleitet, die eben dann nicht mit mit Zirkel und Lineal lösbar ist. download
Kap: Seite 6.2.3: S. 168		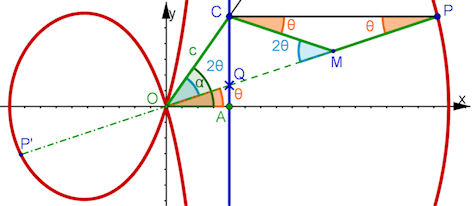Abb. 6.4 Winkeldritteln mit der Konchoide Mit beliebigem a und A = (a, 0) wird der zu drittelnde Winkel alpha an OA angetragen. Der freie Schenkel schneidet die blaue Senkrechte s bei A in Punkt C und c := OC. Mit k := 2c und der "Straße"� s wird die Konchoide gezeichnet. Eine andere Kurve, die die Winkeldrittelung leistet, ist die Trisektrix im GeoGebra-Book    download
	Die klassischen Kurven sind zumeist in im Zusammenhang mit den antiken Problemen entstanden. Der Grundgedanke ist: Hat man eine genaue Zeichnung der betreffenden Kurve, so kann man durch den Schnitt mit dieser die antiken Probleme lösen, diese Lösungen sind mathematisch "gedanklich" exakt. Da man aber mit der Kurve ein "Werkzeug" einsetzt, das über Zirkel und Lineal hinausgeht, gilt diese Vorgehensweise nicht als "streng genug".
Kap: Seite 6.2.4: S. 169		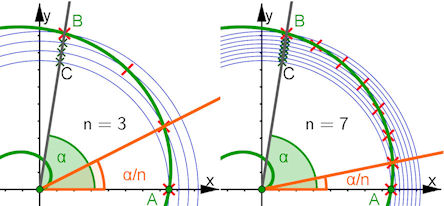Abb. 6.5 Winkeldritteln und n- Teilung mit der archimedischen Spirale: Der zu teilende Winkel alpha wird an OA angetragen, die Kurve schneidet den freien Schenkel in B, der Kreis um O durch A schneidet ihn in C. Eine n-Teilung von Strecke BC ermöglicht eine Kreisschar um den Ursprung O, die aplha/n sichtbar werden lässt. im GeoGebra-Book    download
6.3 Würfel verdoppeln, Delisches Problem
Kap: Seite 6.3: S. 170	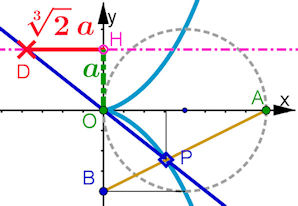Bei jeder Cissoide des Diokles mit A = (c, 0) und der Gleichung (c-x)y^2 = x^3 hat die blau eingezeichnete Gerade die Steigung m = - 1/(3.Wurzel(2))    (Beweis unten im Text des Buches). Daher kann man auf die gezeigte Weise von der Kantenlänge a des alten Würfels zur Kantenlange 3.Wurzel(2) a des neuen Würfels mit doppeltem Volumen gelangen	Abb. 6.6 Dritte Wurzel aus 2 mit Cissoide Im Jahre 430 v. Chr. wütete auf der griechischen Insel Delos die Pest. Die Delier befragten das Orakel von Delphi, was sie zur Besänftigung der Götter tun könnten. Sie erhielten die Aufgabe, fur den würfelförmigen Altar im Tempel einen neuen würfelformigen Altar mit genau doppeltem Volumen zu bauen. In unserer Schreibweise ist also 2 a^3 = x^3 zu losen, das ergibt x = 3.Wurzel(2) a. im GeoGebra-Book    download
6.4 Die konstruierbaren n-Ecke
Kap: Seite 6.4.1: S. 172		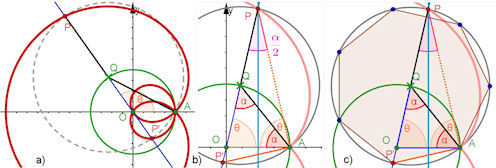Abb. 6.7 a) Strophoide von Freeth: Kurve C ist der Kreis um den Pol O mit dem Radius a durch den festen Punkt A = (a, 0). b) Die Mittelsenkrechte von Strecke OA schneidet die äußere Strophoide in einem Punkt, auf den man P durch Ziehen an Q setzt. Die besonderen Eigenschaften dieser P-Stellung sind gezeigt und werden im Text bewiesen.
	c) alpha ist der Mittelpunktswinkel eines 7-Ecks, dessen orangefarbene Seite P'A im grauen Kreis um Q schon erzeugt ist. GeoGebra bietet einen Button fur regelmäßige n-Ecke an. Aus der Seite P'A wird damit das regelmäßige 7-Eck gebildet. Es hat seine Ecken tatsächlich auf dem grauen Kreis.	im GeoGebra-Book    download
6.5 Kreis quadrieren, pi konstruieren
Kap: Seite 6.5.2: S. 175		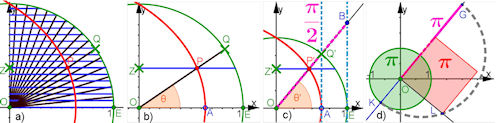Abb. 6.8 a) Quadratrix: Punkt Z = (0, z) und Q = (1; theta) (polar geschrieben) starten auf der x-Achse. Sie wandern auf der y-Achse bzw. dem Einheitskreis und bewegen sich gleichmäßig so, dass sie gemeinsam im Punkt (0,1) ankommen. Mit dem gezeigten Raster findet man Punkte der Quadratrix.
	b) Eine typische Stellung ist hervorgehoben. c) Das Ziel, pi zu finden, ist erreicht. d) Am Ende ist der Kreis quadriert, also ist ein Quadrat mit dem Flächeninhalt pi entstanden, wie ihn auch der Einheitskreis hat. Aber es ist keine zulässige Konstruktion mit Zirkel und Lineal.	im GeoGebra-Book    download
6.6 Quasikonstruktion=... mit Zirkel Lineal und Parabellineal www.mathematik-verstehen.de
Kap: Seite 6.6.1.1: S. 177		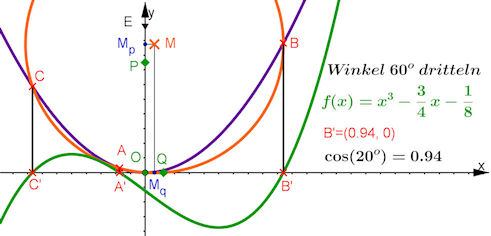Abb. 6.9 Polynomlösung mit Zirkel, Lineal und Parabellineal: Mq ist Mittelpunkt von Strecke OQ und Mp ist Mittelpunkt von Strecke EP mit E = (0, 1). So ist M für den Kreis durch O konstruiert. Die ein bis drei anderen Schnittstellen von Parabel und Kreis sind die Lösungen. Diese Quasikonstruktion ist hier gezeigt für das 3-Teilungspolynom von 60°. im GeoGebra-Book    download
Kap: Seite 6.6.2: S. 178		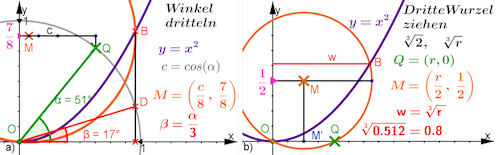Abb. 6.10 Quasikonstruktionen, die von der Fragestellung allein mit Zirkel, Lineal und Parabellineal zur Lösung gelangen: a) Winkel alpha ist mit zugfestem Q auf dem Einheitskreis gegeben. Durch Achtelungen zweier Stecken erhält man M für den Kreis, der die Normalparabel schneidet, Schnittpunkt B liefert sofort das Drittel von alpha.
	b) Der Radikand r wird als Abszisse von Q genommen, durch Mittelung ergibt sich M' und dann M mit der Ordinate 1/2 . Der Schnittpunkt des Kreises um M durch O und der Normalparabel hat als Abszisse den gesuchten Wert w = 3.Wurzel(3).	im GeoGebra-Book    download
6.7 Archimedes hat ein antikes Flächenproblem gelöst
Kap: Seite 6.7: S. 179		Abb. 6.11 Das Parabelsegment nach Archimedes nimmt 2/3 des Parallelogramms ein, siehe Satz 6.4. Zwischen dem Beweis von Archimedes und der Schreibweise rechts vergingen 2000 Jahre. Unser Konzept des Integrals leistet allerdings sehr viel mehr.
Kap: Seite 6.7: S. 179		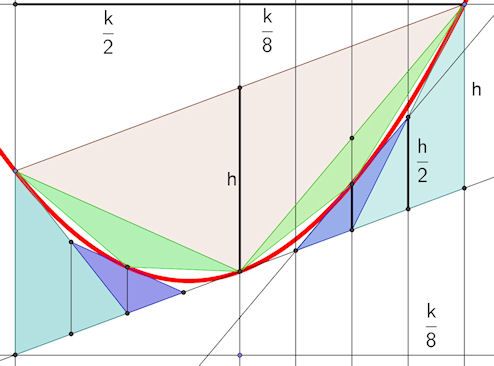Abb. 6.12 Archimedes, Quadratur der Parabel Immer mehr grüne und blaue Dreiecke schließen die Parabel ein. Das Parabelsegment nimmt dann 2/3 des Parallelogramms ein. im GeoGebra-Book    download

Prof. Dr. Dörte Haftendorn	Erstellt August 2016, Update 20.03.2018	www.kurven-erkunden-und-verstehen.de