Allgemeines

3.1 Konchoiden

3.2 Strophoiden

3.3 Cissoiden

3.4 Trisektrix

3.5 Analysis hierzu

Verallgemeinerte Kurvendefinitionen
Es gibt für die drei klassischen Kurvenfamilien allgemeine Definitionen, die die ganze Vielfalt in sich tragen. Im Buch habe ich nicht gewagt diese voranzustellen, hier aber zeige ich sie nebeneinander. Es gibt eine Kurve C (oder zwei C1 und C2). Auf C läuft ein zugfester Punkt Q. Es gibt einen Pol B (meist der Ursprung), von dem ein Radiusstrahl ausgeht. Auf diesem liegt der Punkt P, dessen genaue Lage sich auf je besondere Weise aus Q ergibt. Die Ortskurve von P ist die gesuchte Kurve.
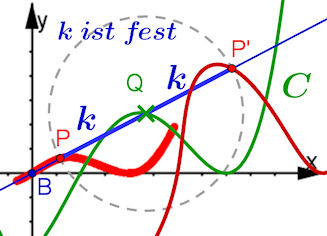
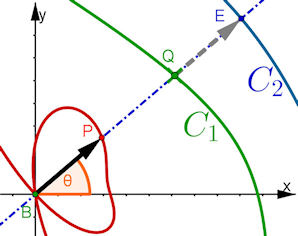
Allgemeine Konchoide Der Kreis um Q hat den festen Radius k. Bei der Konchoide des Nikomedes ist C eine Gerade. Bei den Pascalschen Schnecken ist C ein Kreis. im GeoGebra-Book    download	Allgemeine Strophoide Der Kreis um Q muss A enthalten. im GeoGebra-Book    download	Allgemeine Cissoide Der Vektor auf dem Radiusstrahl, der von C1 nach C2 weist, wird an den Pol angehängt. Bei der Cissiode des Diokles ist C1 ein Kreis und C2 eine bestimmte Gerade. Mit dieser Cissoidendefinition erreicht man auch die Konchoide des Nikomedes, die Standard-Strophoide und die Trisektrix. im GeoGebra-Book    download
Mehr zu Konchoiden	Mehr zu Strohoiden	Mehr zu Cissoiden

3.3 Trisektrix des Maclaurin
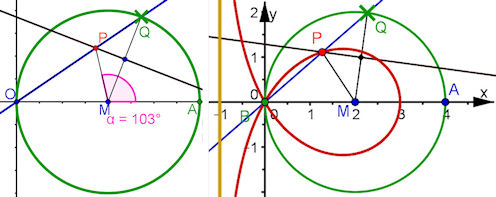
Kap: Seite 3.3: S. 62		Abb. 3.16 Trisektrix von Maclaurin Der Winkel alpha soll gedrittelt werden. Zum selbst Erkunden im GeoGebra-Book    download Zum Vortragen Trisektrix edel (Vortrag) Beweisschritte (ausführlich im Buch) Gesamtbeweis-Ansicht download Zum schrittweise Dazunehmen download
3.5 Analysis-Anwendungen bei den klassischen Kurven
Kap: Seite 3.5: S. 75 Bspl. 3.1		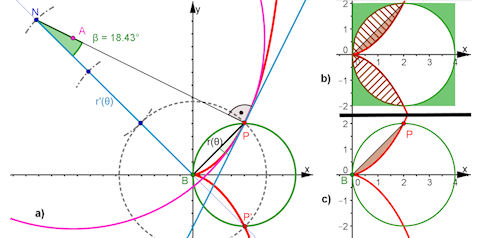Beispiel 3.1, darin Abb. 3.27 Man sieht die besonderen Zusammenhänge. Die Lage von N auf der Senkrechten zum Polarradius hat den Wet der Ableitung. Beweis im Buch Seite 320. Zum Punkt A, dem Mittelpunkt des Krümmmungskreises, ist in Beispiel 3.6 die Lage bewiesen. Bei der Königin der Spriralen fallen A und N zusammen. (Kap. 8.1.2.3, S 229). Die Flächen sind nachfolgend betrachtet download
Kap: Seite 3.5: S. 75		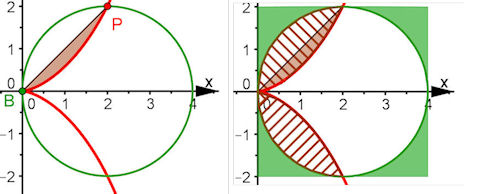Beispiel 3.1, darin Abb. 3.27 b) und c) Besondere Flächen. im GeoGebra-Book    download Wenn man nicht integrieren kann, erhält man mit vielen Punkten auf Kreis und Cissoide auch eine ordentliche Näherung. In der der Datei ist kartesisch integriert, es wäre bei der Cissoide aber auch gut "polar" gegangen, wie es im Buch bemacht ist. Dann ist die Integration einfach, der Kreis ist elementargeometrisch bewältigt.
Kap: Seite 3.5: S. 76f	Weitere Beispiele zur Analysis der klassischen Kurven: Bspl. 3.3 Kreisfläche und Stolpersteine bei der Berechnung als Polarfläche Bspl. 4.4 Fläche der Kardioide Bspl. 3.5 Bogenlänge der Kardioide und Integrations-Lerneffekte	Elemente der Analyis für Kurven Herleitungen und Formeln

Prof. Dr. Dörte Haftendorn	Erstellt August 2016, Update 20.03.2018	www.kurven-erkunden-und-verstehen.de