8.1 Spiralen

8.2 Rosetten

8.3 Rollkurven

8.4 Schwingungen

8.1 Spiralen
Kap: Seite 8.1: S. 219		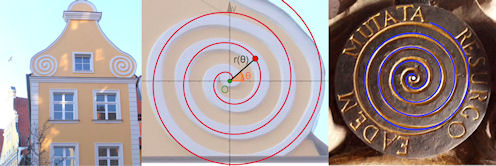Abb. 8.1 Spiralen des Barock, Abschnitt 8.1.1: a) Haus in Stralsund b) Anpassung mit einer archimedischen Spirale c) Epithaph für Jakob I. Bernoulli in Basel (Quelle: eigene Fotos)
Kap: Seite 8.1: S. 220		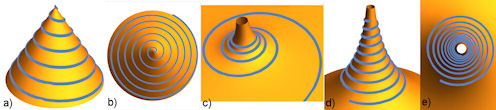Abb. 8.2 Seile werden um Rotationskörper gewickelt. a) und b) Kegel mit Seil ergibt die archimedische Spirale, c) Hyperboloid mit Seil ergibt die hyperbolische Spirale, siehe Abb. 8.11 in Abschnitt 8.1.3.2, d) und e) Logarithmus-Rotationskörper (gespiegelt) ergibt die logarithmische Spirale, siehe Abschnitt 8.1.2
Kap: Seite 8.1.1: S. 221		Abb. 8.3 Archimedische Spiralen in polar-kartesischer Darstellung: a) Hauptform polar b) kartesisch als Ursprungsgerade c) archimedische Spirale mit einem Zentralkreis d) kartesisch als nach oben verschobene Gerade.
	a)im GeoGebra-Book    Archimedische Spirale download b) im GeoGebra-Book     Archimedische Spirale mit Zentralkreis download
Kap: Seite 8.1.1: S. 222		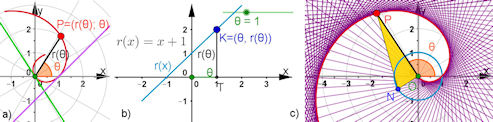Abb. 8.4 Tangenten an archimedische Spiralen in polar-kartesischer Darstellung: a) polar mit zwei Tangenten b) kartesisch mit der Geraden r(x) = x + 1 für -1<=theta c) geometrische Tangentenkonstruktion
	a) und b) download     c) im GeoGebra-Book    c) Tangenten-Konstruktion download
Kap: Seite 8.1.1.2: S. 223		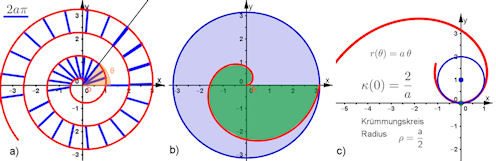Abb. 8.5 Eigenschaften der archimedischen Spirale: a) Ab theta=2Pi haben benachbarte Spiralarme den konstanten Radialabstand 2aPi. b) Der Spiralarm für 0<theta< 2Pi nimmt in der gezeigten Weise ein Drittel der Fläche des umfassenden Kreises ein. c) Der Krümmungskreis fur den Ursprung hat den Radius rho = a/2. Gezeigt ist r(theta) = 2theta fur -1
	a) download      b) download      c) download
8.1.2 Königin der Spiralen = Exponential-Spirale = logarithmische Spirale = gleichwinklige Spirale = Bernoulli'sche Spirale = spira miabilis = Spirale der Natur Eine Erklärungung aller dieser synonymen Namen finden Sie im Buch.
Kap: Seite 8.1.2: S. 224		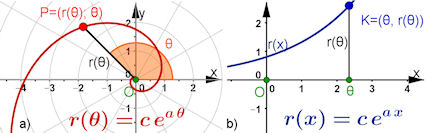Abb. 8.6 Die Königin der Spiralen hat viele Namen: Logarithmische Spirale Exponential-Spirale Gleichwinklige Spirale Bernoulli’sche Spirale spira mirabilis im GeoGebra-Book    download
Kap: Seite :8.1.2 S. 225		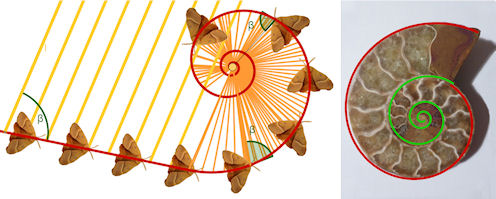Abb. 8.7 Gleichwinklige Spirale für Nachtfalter und Ammoniten (Quelle für einzelnen Wollraupenspinner: Wikipedia, für Ammonit: eigenes Foto) a) im GeoGebra-Book    a) download b) download
Kap: Seite 8.1.2.1: S. 225		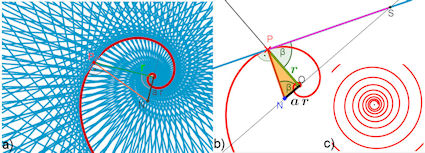Abb. 8.8 Tangenten der gleichwinkligen Spirale a) Tangentenmuster b) Tangentendreieck und der Grenzwert der Spiralenlänge von P bis O = Strecke PS c) Ausschnitt in Ursprungsnähe b) im GeoGebra-Book    b) download c) download
Kap: Seite 8.1.2.4: S. 228		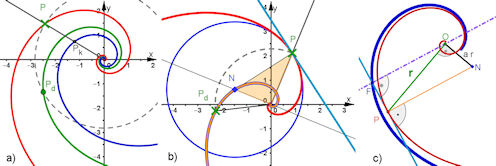Abb. 8.9 Königin-Spirale: a) Drehen und Strecken sind austauschbar b) Tangentenkonstruktion mit Krümmungskreis um N und Ortskurve von N (Evolute) als gedrehte Ausgangsspirale c) Die Fußpunktkurve einer Königin-Spirale ist wieder eine Königin-Spirale.
	a) im GeoGebra-Book    a) download      b)im GeoGebra-Book    b) download    c) im GeoGebra-Book    c) download
8.1.3.2 Systematisierung der Spiralen nach Funktionstyp
Kap: Seite 8.1.3.2: S. 231		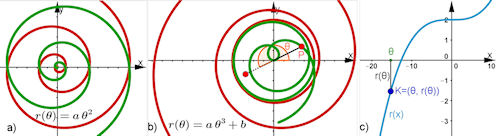Abb. 8.10 a) Parabel-Spirale (Galilei’sche Spirale) b) und c): Die nach oben verschobene „Sattelfunktion“ r(x) = 0.001x^3 + 2 erzeugt für negative Winkel eine interessante Extraschleife im GeoGebra-Book    download im GeoGebra-Book    download
Kap: Seite 8.1.3.2: S. 232		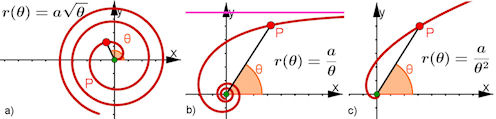Abb. 8.11 Potenzspiralen a) Wurzel-Spirale von Fermat b) Hyperbel-Spirale oder hyperbolische Spirale mit ihrer Asymptote c) Kehrwert-Parabel-Spirale, die keine Asymptote hat, Beweis im Absatz: Hyperbelspirale.
	a) im GeoGebra-Book    a) download b) im GeoGebra-Book    b) download     c) im GeoGebra-Book    c)download
Kap: Seite 8.1.3.2: S.232		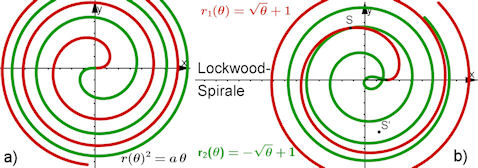Abb. 8.12 noch mehr Spiralen a) Wurzelspirale mit beiden Ästen b) Lockwood-Spirale aus verschobener Wurzelfunktion mit beiden Ästen, vorgestellt von [Lockwood 1961]. Dort hat die Wurzel noch den Faktor 2. b) im GeoGebra-Book    b) download
Kap: Seite 8.1.3.2.: S. 233		Abb. 8.13 Lituus, Krummstab, Bischofsstab, ionisches Kapitell mit der Polargleichung r(theta) = c/ Wurzel(theta). im GeoGebra-Book    download
Kap: Seite 8.1.3.2: S. 233		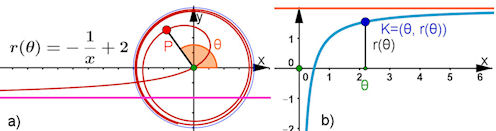Abb. 8.14 Kreis und Gerade als Spiral- Asymptoten. Durch Verschieben der gespiegelten Hyperbel ergeben sich einige Überraschungen. im GeoGebra-Book    download
Kap: Seite 8.1.3.2: S. 234		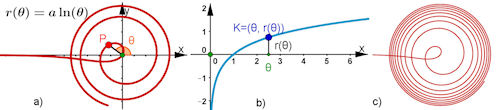Abb. 8.15 Logarithmus-Spirale: a) Polarkurve zu r(theta) = ln(theta), b) kartesische Funktion dazu, c) ohne Achsen mit vielen Windungen, die sich prinzipiell nicht in einem Kreis „einfangen“ lassen. im GeoGebra-Book    download
Kap: Seite 8.1.3.3: S. 235		Abb. 8.16 Juliamengen, wie sie in Korrespondenz zu Punkten c in der komplexen Ebene des „Apfelmännchens“ auftreten, enthalten oft näherungsweise die Königin-Spiralen: Links für c = 0.764 - 0.125 i, rechts für c = 0.819 - 0.194 i http://www.mathematik-verstehen.de Bereich Fraktale Geometrie ->Apfelmännchen, Juliamengen
8.2 Rosetten oder Rosenkurven
Kap: Seite 8.2: S. 236		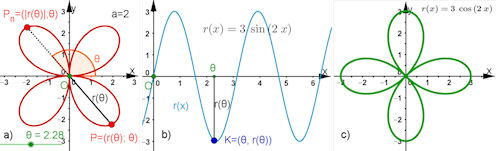Abb. 8.17 Grundlage fur Rosetten: a) Polarkurve zu r(theta) = 3 sin(2 theta), b) kartesische Funktion dazu, c) nimmt man den Kosinus statt des Sinus, dreht man lediglich um 45°. im GeoGebra-Book    download
Kap: Seite 8.2.1.1: S. 237		Abb. 8.18 Rosetten mit Umkreisradius c und ganzzahligem Faktor a, wie er am Bild notiert ist. Es sind Plus- und Minus-Blätter in der Zeichenreihenfolge beschriftet. GeoGebra-Datei wie zu Abb.8.17
Kap: Seite 8.2.1.1.: S. 238		Abb. 8.19 Rosetten mit gebrochenem Parameter: im GeoGebra-Book    download
Kap: Seite 8.2.1.2: S. 239		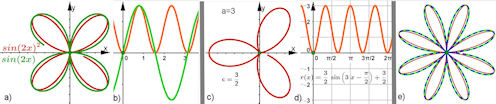Abb. 8.20 Rosetten variiert: a) und b) in Grün die Urform des Quadrifolium, der Vierblattrosette, polar und kartesisch gezeigt. Die roten Blätter gehören zur quadrierten Sinusfunktion. Sie haben gleiche Öffnungswinkel und längste Erstreckung, sind aber schmaler. Am kartesischen Graphen sieht man, dass sie vom 1. Quadranten aus in mathematisch positivem Sinn gezeichnet werden.
	c) und d) zeigen ein Trifolium, das zu einer verschobenen Sinusfunktion gehört ( siehe Gleichung 8.9). Bild e) zeigt blau-grün-gestrichelt die Blätter der Urform für a = 4 und die zum Betrag der Sinusfunktion gehörigen Blätter genau aufeinander. Innen aber sind in Rot schmaler die Blätter der Quadratform der Gleichung.	im GeoGebra-Book    download
Kap: Seite 8.2.1.2: S. 240		Abb. 8.21 Rosetten mit Plus-Blättern nach der Gleichung 8.9 r(theta) = c sin^2 ( a/2 theta ) mit c = 3. Die Rosette für a = 3 ist in Abb. 8.20 c) zu sehen. GeoGebra-Datei wie zu Abb.8.20
Kap: Seite 8.2.2: S. 240	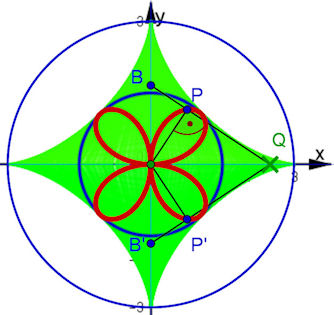Abb. 8.22 Rosette als Fußpunktkurve der Astroide Im Abschnitt 4.4.5.2 und Abb. 4.37 b) ist die Astroide als Hüllkurve einer Stange fester Länge zu sehen, deren Enden auf den Achsen wandern. Im genannten Bild wird eine Ellipse erzeugt, links aber wird vom Ursprung aus ein Lot auf die Stange gefällt. Der Fußpunkt dieses Lotes sei P, an der x-Achse gespiegelt liegt P’.	Die Ortskurve von P ist das Quadrifolium, die übliche Vierblatt-Rosette aus Abb. 8.17, wie im Folgenden bewiesen wird. Hier ist die Astroide der Rand der grünen Fläche. Ihre Gleichung wird nicht benötigt, denn mit der Stange hat man ja schon die benötigten Tangenten. im GeoGebra-Book    download
Kap: Seite 8.2.3.1: S. 241		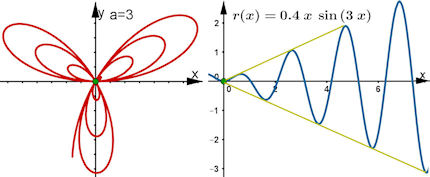Abb. 8.23 Die Propeller-Blüte verknüpft die archimedische Spirale mit der Rosette. Zwischen zwei kartesischen Geraden „pendelt“ ein Sinusgraph mit immer größer werdender Amplitude. Die Blätter „erben“ von der archimedischen Spirale, dass ihre Scheitel stets um das gleiche Stück nach außen rücken. im GeoGebra-Book    download
Kap: Seite 8.2.3.2: S. 242		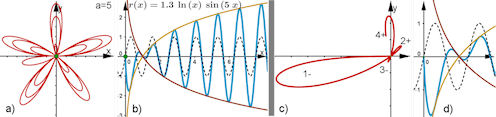Abb. 8.24 Logarithmus-Blume mit Extrazipfel r(theta) = c ln(theta) sin(a theta) mit a = 5 und c = 3 im GeoGebra-Book    download
Kap: Seite 8.2.3.3: S. 242		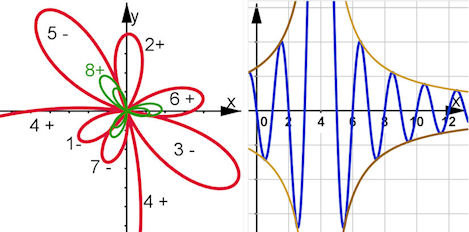Abb. 8.25 Hyperbel-Blume r(theta) = 1 /(theta-4) sin(pi theta) Wenn theta eine natürliche Zahl ist, wird der Sinusterm Null, außer für theta = 4, denn dann ist auch der Nenner Null. Als Grenzwert ergibt sich fur x �gegen 4 der Wert pi. Also hat das Blatt 4+, das sich im III. Quadranten erstreckt, in der Richtung theta = 4 = 229, 2° den Polarradius pi. Das sieht man nicht, da das Bild links nur bis x = -1 reicht. im GeoGebra-Book    download
8.3 Rollkurven
Kap: Seite 8.3.1: S. 243		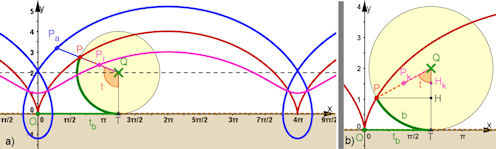Abb. 8.26 Zykloide, k ist der Streckfaktor, der Pk auf dem Radiusstrahl des Rollkreises festlegt: a)in Rot: gespitzte Zykloide mit k = 1 , in Blau: verlängerte Zykloide für außerhalb des Rollkreises gelegene Punkte Pk für k > 1, in Violett: verkürzte Zykloide für innerhalb des Rollkreises gelegene Punkte Pk mit k < 1, hier als Pa und Pi bezeichnet. b) Beweiszeichnung für die Parameterdarstellung mit dem Parameter t. im GeoGebra-Book    download
Kap: Seite 8.3.1.2: S. 245		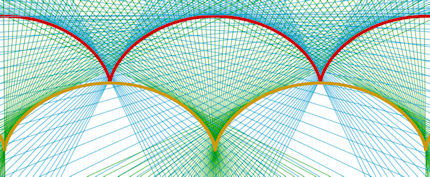Abb. 8.27 Zykloide und ihre Evolute Zu der roten Zykloide ist in Blau die Tangentenschar und in Grün die Normalenschar gezeichnet. Die Hüllkurve der Normalen (Abschnitt 9.3) ist die Evolute der Zykloide. Sie ist erstaunlicherweise wieder eine Zykloide, hier ockerfarben eingezeichnet. im GeoGebra-Book    download
Kap: Seite 8.3.2: S. 247		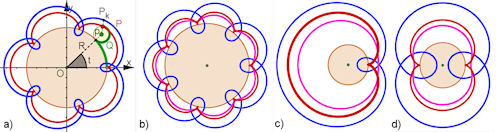Abb. 8.28 Epitrochoide In Rot sind gespitzte (k = 1), in Blau verlängerte (k > 1) und in Violett verkürzte (k < 1) Epitrochoiden dargestellt. Mit m = R . gilt für a) m = 5, b) m = 7, c) m = 1, die Kardioide für k = 1, d) m = 2, die Nephroide für k = 1. Zu c) und d) siehe Abschnitt 9.4. im GeoGebra-Book    download
Kap: Seite 8.3.2: S. 248		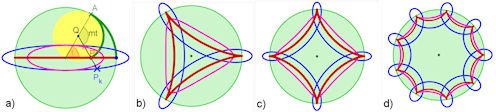Abb. 8.29 Hypotrochoiden In Rot sind gespitzte, in Blau verlängerte und in Violett verkürzte Hypotrochoiden dargestellt. Mit m = R . gilt für a) m = 1, eine Strecke für k = 1, sonst Ellipsen, b) m = 3 und Steiner’sche Kurve für k = 1 (Aufgabe 9.4), c) m = 4 und Astroide für k = 1 (Abschnitt 9.2.4), d) m = 9. im GeoGebra-Book    download
Kap: Seite 8.3.2: S. 248		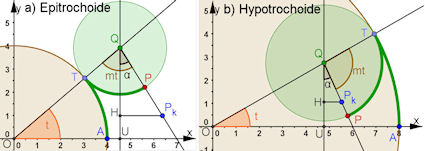Abb. 8.30 Beweiszeichnungen für Epi- und Hypotrochoide, Rastkreisradius R, Rollkreisradius rho, Quotient m = R/rho>1 a) Winkel(TQP) = phi, b) WInkel(PQT) = phi Beweiszeichnungen download   download
Kap: Seite 8.3.3: S. 249		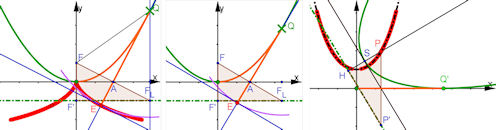Abb. 8.31 Eine Parabel soll auf der x-Achse abrollen. im GeoGebra-Book    download Darin ist auch die CAS-Brechnung des Integrals.
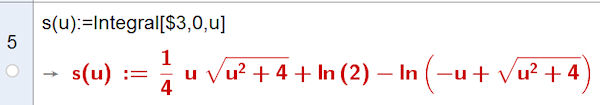
	a) Vorarbeit: Punkt Q wandert auf einer festen Parabel mit Brennpunkt F und Parameter p. Die Leitgerade ist F'FL . Auf der Tangente in Q wird die durch Integration berechnete Bogenlänge vom Scheitel bis Q als Strecke QE abgetragen. Als Nebeneffekt ist in Rot eine Evolvente der Parabel markiert. Bild b) Die Konstruktion aus a) wird zum "Lieferanten"� für gewisse Abstände, die in Bild c) gebraucht werden. Dabei soll E der Koordinatenursprung werden, EQ wird x-Achse. Bild c) In diesem 2. Grafikfenster soll die rollende Parabel entstehen. Strecke EQ definiert den Berührpunkt Q' und der Brennpunkt P = (Strecke EA, Strecke AF) wird eingetragen. Da das Dreieck FLFF' mit rechtem Winkel bei F' kongruent als Dreieck P' PH übertragen werden soll, konstruieren wir H mit dem Thaleskreis uber PP' und dem Parabelparameter Strecke HP = p = F'�F. Parabelachse ist dann HP und HP' ist Leitgerade. Mit dem Befehl "Parabel aus Brennpunkt und Leitgerade" erhält man die grüne Parabel. Wird nun im linken Grafikfenster, also in Bild b), Punkt Q auf der (festen) Parabel bewegt, so rollt im rechten Grafikfenster, Bild c), die kongruente grüne Parabel auf der x-Achse ab und hat dabei den Berührpunkt Q'. Die Ortslinie des Brennpunktes ist als Spur rot markiert, schwarz gestrichelt ist die Kettenlinie (Kosinus hyperbolicus Funktion) eingetragen. Sie passt dazu.
8.3.3.3 Zentrale Idee dieses Vorgehens bei Rollkurven Bewegt man sich bei den Rollkurven über Kreise und Geraden hinaus, kommt man um eine Integration zur Längenbestimmung nicht herum. Hier ist bemerkenswert, dass zunächst bequem die Tangente auf der Parabel abrollt und die entstehenden Längen dann im 2. Grafikfenster helfen, die umgekehrte Situation zu meistern, nämlich die Parabel auf einer festen Geraden abrollen zu lassen. Links: Offenbar faszinieren Rollkuven – und Kurven überhaupt – auch etliche Internetautoren. Den [Famous Curves Index] http://www-history.mcs.st-and.ac.uk/Curves/Curves.html konnte man schon 1998 nutzen, neuer sind [2dcurves Website] http://www.2dcurves.com/und [Xah Lee Website]. http://xahlee.info/SpecialPlaneCurves_dir/specialPlaneCurves.html Letztere Site zeigt schön gestaltete Animationen zu den Kurven dieses Kapitels unter den Überschriften cyclodal curves und roulettes.
8.4 Schwingungen
Kap: Seite 8.4.1: S. 251		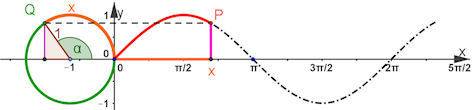Abb. 8.32 Sinusfunktion aus dem Einheitskreis gewinnen. Die Ordinate von Q wird sin(x) genannt: also P = (x, sin(x)). im GeoGebra-Book    download
Kap: Seite 8.4.1: S. 251		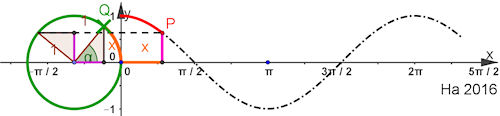Ergänzung zu Abb. 8.32 Kosinusfunktion aus dem Einheitskreis gewinnen. Die Abszisse von Q wird cos(x) genannt, sie wird durch eine 90°-Drehung übertragen: also P = (x, cos(x)). im GeoGebra-Book    download
Kap: Seite 8.4.1: S. 251		Ergänzung zu Abb. 8.32 Tangensfunktion aus dem Einheitskreis gewinnen. Der Randiusstrahl duch Q schneidet die Tangente im O in (0, tan(x)): also P = (x, tan(x)). im GeoGebra-Book    download
8.4.2 Lissajous-Kurven
Kap: Seite 8.4.2.1: S. 252		Abb. 8.33 Lissajous-Kurven für x(t) = 3 sin(t-phi) und y(t) = sin(5t). Der graue Punkt gehört zu t = 0.8
	a) für phi = 0, b) und c) für phi = 0.2, c) 3D-Darstellung der "1 : 5-Krone". Für 0 <= t < 2 pi/3 ist die Kurve in Rot gezeichnet, für 2 pi/3 <= t < 4 pi/3 in Grün und für 4 pi/3 <= t < 2 pi in Blau. Im Buch wird erkläsrt, wie und warum man in der 3D-Version eine ganze Familie von Lissajouskurven verstehen kann.	im GeoGebra-Book    download
Kap: Seite 8.4.2.2: S. 252		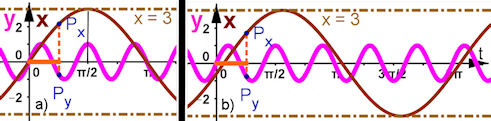Abb. 8.34 Definierende Funktionen zu Abb. 8.33 kartesisch dargestellt. x braun, y violett a) phi = 0 und b) phi = 0.2 GeoGebra-Datei zu Abb.8.33 im 2. Grafikfenster
Kap: Seite 8.4.2.4: S. 253		Abb. 8.35 Lissajous-Kurven für x(t) = 3 sin(2t) und y(t) = sin(5t), also für phi = 0. Der graue Punkt gehört zu t = 2.8. a) 2D-Lissajous-Kurve, b) 2 : 5-3D-Lissajous-Krone, c) kartesische Darstellung der definierenden Funktionen Alles ist in den beiden Grafikfenstern und dem 3D derselben Datei im GeoGebra-Book    download

Prof. Dr. Dörte Haftendorn	Erstellt August 2016, Update 1.05.2018	www.kurven-erkunden-und-verstehen.de