| 02 Wekzeugkasten
2.7 und 2.8 GeoGebra und andere Software |
| Website zum Buch: Hier sind die Dateien, die die Bilder des Buches erzeugt haben, die Aufgabenlösungen, Beweis-Ergänzungen und weitere Kurven, für die im Buch kein Platz mehr war. Wenn Sie hier etwas nicht verstehen, lesen Sie im Buch. Falls Sie Fehler finden ober noch Fragen übrig sind, wenden Sie sich an mich. |
| 2.1-2.2 Grundlage | 2.3 Polar |
2.4 Parametrisch | 2.5 Typen und 3D |
2.7-2.8 GeoGebra u. a. Software |
|||||
| GeoGebra und GeoGebra-Book | Kurvenbefehle | CAS | Mehrere Grafikseiten | TI-nspire |
| Mathematica | wolfram-alpha | Surfer | Cabri3D, Archimedes | Cinderella |
| Kap: Seite 02: S. 31 |
 | http://www.geogebra.org | |||||||
| Kap: Seite 02: S. 31 |
 | ||||||||
| Kap: Seite 02: S. 32 |
 | https://www.geogebra.org/search/haftendorn
Auf meinem Bereich bei GeoGebra stehen mehrere GeoGebra-Books von mir. Für das Buch Kurven erkunden und verstehen gibt es auch ein solches Book. Dort finden Sie zu allen interaktiven Bildern meines Springer-Buches die Applets, die dann bei GeoGebra auf dem Server laufen. Ich empfehle Ihnen aber wärmstes sich selbst GeoGebra zu beschaffen und die *.ggb-Dateien von hier oder aus dem GeoGebra-Book herunterzuladen. Dann haben Sie bequemen Zugriff auf alle Möglichkeiten. | |||||||
| Kap: Seite 02: S. 32 |
 | Klichen Sie also so ein Element an. Dann öffnet GeoGebra eine interative Seite dazu, das Applet. Wenn Sie mit allen Möglichkeiten von GeoGebra weitermachen wollen, gibt es oben rechts den Button zum Download der *.ggb-Datei. Es ist i.d.R. dieselbe, die Sie auf dieser Site finden.
Z.Z. gibt es noch Probleme mit den Dateien, die direkt 3D-Grafik zeigen sollen. Nehemn Sie dass die *.ggb selbst. | |||||||
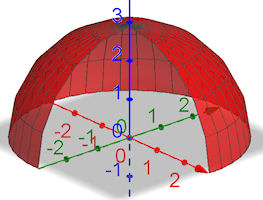 | |||||||||
| Kap: Seite 04: S. 81 |
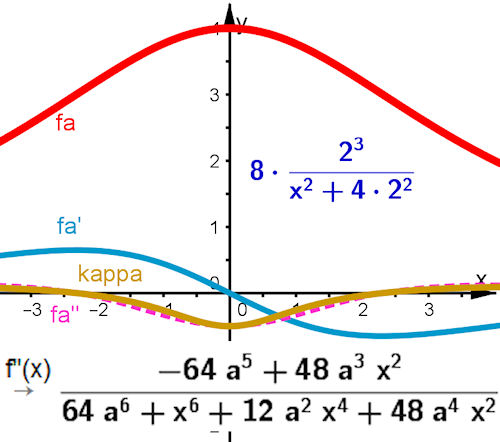 | Abb. 4.2
Vollständige Berechnung der Krümmung der Versiera mit GeoGebra-CAS.
Achtung: im CAS definiert f(x):=8 a^3/(x^2+4 a^2) mit Doppelpunkt und a im Algebra-Fenster aber fa(x)=8 r^3/(x^2+4 r^2) ohne Doppelpunkt und r als Schieberegler. Das ist notig, weil man man sonst im CAS den Parmeter nicht sehen kann. Es ist aber wichtig, dass man die Ableitungsterme und die Kümmung in Abhängigkeit vom Parameter erhält. Dies wird im Buch Seite 81f wirklich ausgenutzt.
| |||||||

| |||||||||
| Kap: Seite 02: S. 33 |
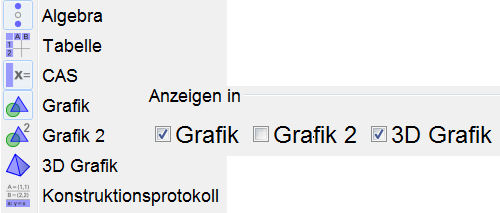
| Die Möglichkeit mehrere Fenster zu verwenden wird - meiner Beobachtung nach - sehr wenig genutzt. In diesem Buch aber kommt sie in der polar-kartesischen Darstellung von Polarkurven, in der doppelt-kartesischen Darstellung von Parameterkurven und bei den Bipolaren Kurven und ihrer Dreiecksbedingung ausfühlich und letztlich unverzichtbar vor.
Zuerst macht im Menu Ansicht Grafik 2 auf. Neue Objekte landen dort, wenn man das Fenster aktiviert. Im Dialog Eigenschaften eines Objektes kann man die Stellung nachträglich noch verändern, z.B. es in beiden Fenstern sichtbar machen. | |||||||
| |||||||||
| Kap: Seite 02: S. 35 |
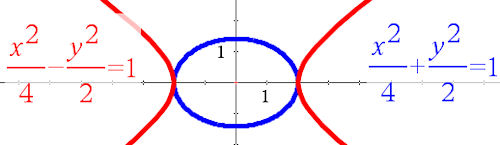
https://education.ti.com/de/deutschland/home Dort ist bei Service auch ein Lehrer.Prüfpreis-Angebot. Weiter sind Materialen verfügbar. Weitere Infos | Mit dem TI-Nspire CX CAS in der Hand der Lernenden kann didaktisch wertvolle Eigentätigkeit in den Unterricht integriert werden. Die Geometrischen Konstruktionen dieses Buches lassen sich realisieren, auch die Ortslinien. Bedauerlicherweise gibt es aber z.Z. (2016) nur sehr eingeschränkte Möglichkeiten für implizite Gleichungen. Sie heißen dort Relationen, aber verfügbar sind nur Kegelschnitt-Gleichungen, lineare Gleichungen (sind ja auch Kegelschnitte) und Formen vom Typ y=f(x) und x=g(y). Von den Anforderungen dieses Buches sind Parameterkurven und Polarkurven verfügbar.
| |||||||
| Kap: Seite 02: S. 35 |
 | Mathematica ist ein sehr umfangreiches CAS (Computer-Algebra-System) http://www.wolfram.com http://www.wolfram.com/mathematica/ Begonnen hat vor mehr als 30 Jahren Steven Wolfram in USA. Inzwischen ist daraus eine große Firma geworden mit einem riesigen Stab an kompetenten Mitarbeitern. In Deutachland wird Mathematica vertrieben von der Firma Additve. Es gibt inzwischen halbwegs bezahlbare Lizenzen für Lehrer, Schüler und Studenten. Senioren zahlen die Hälfte!. | |||||||
 http://mathworld.wolfram.com
http://mathworld.wolfram.comist ein sehr ausführliches und ziemlich zuverlässigens frei zugängliches mathematisches Lexikon, das von der Mathematiker-Community beobachtet wird. Man sollte es immer außer Wikipedia auch benutzen. In diesem Buch sind viele 3D-Grafiken und wirklich "harte" Rechnungen mit Mathematica gemacht. Speziell für dieses Buch ist http://mathworld.wolfram.com/topics/Curves.html besonders relevant. | |||||||||
| Kap: Seite 02: S. 35 |
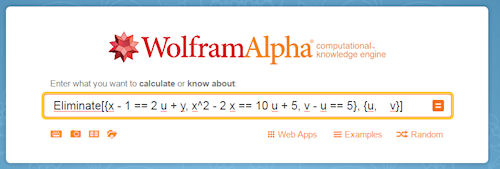 | Wolfram Alpha ist eine kostenlose Plattform im Internet, die für einzeilige Befehle die ganze Macht von Mathematica, eines der weltweit bedeutensten CAS, zur Verfügung stellt. Dieses ist m.E. viel zu wenig bekannt.
Bei http://www.wolfram-alpha.com erhält man die gezeigte Eingabezeile, in die man Befehle eintragen kann. Hier ist des Beispiel mit dem in diesem Buch oft verwendeten Befehl Eliminate[...] | |||||||
| Kap: Seite 02: S. 35 |
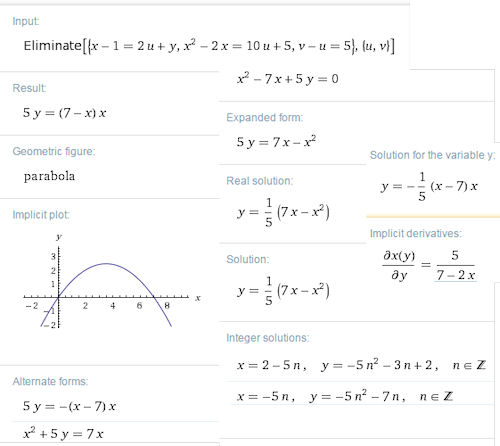 | Die Fülle an Informationen ist erstaunlich. In diesem Buch braucht man den Befehl Eliminate immer wieder. Wenn dann eine wirklich lange Gleichung für die gesuchte Kurve herauskommt, kann man die mit "copy as plaintext" direkt in die GeoGebra-Eingabezeile übernehmen. Man muss dann nur das doppelte Gleichheitszeichen == durch ein einfaches = ersetzen. Es gibt im Buch Gleichungen, die hätte ich in erträglicher Zeit nicht von Hand herausbekommen, z.B. die Gleichung der Cover-Kurve Seite 49 oder die der Topfblume Seite 137. | |||||||
| Kap: Seite 02: S. 1 |
  | Der Mathematiker Oliver Labs hat zum Jahr der Mathematik 2008 für das Forschungszentrum Oberwolfach die Raumflächen-Software Surfer entwickelt, die frei verfügbar ist. http://www.imaginary2008.de/ surfer.php?lang=en Direkt: https://imaginary.org/program/surfer#all-downloads Labs, Oliver: Website, 3D-Druck. http://www.oliverlabs.net In Blau ist die algebraische Raumflächhe gezeigt: (x-b-a^2)*(x-b+a^2)*(x+b-a^2)*(x+b+a^2)+y^2-z^2=0 | |||||||
| Kap: Seite 02: S. 1 |
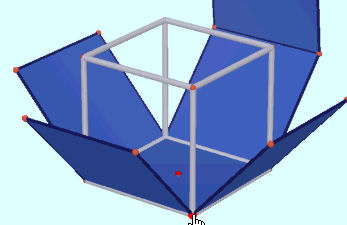 | Cabri Geomètre ist die Urmutter aller DGS Heute heißt die 2D-Version Cabri II Plus. Die TI-Geometrie ist ein Nachkömmling von Cabri. Mit Cabri 3D www.cabri.com. werden neue Wege beschritten, die andere 3d-Programme für das Lernen noch nicht so ausfühlich bieten. Experte ist Prof. Heinz Schumann http://www.mathe-schumann.de/geometrie-seite/. Cabri 3D muss man kaufen. | |||||||
| Kap: Seite 02: S. 1 |
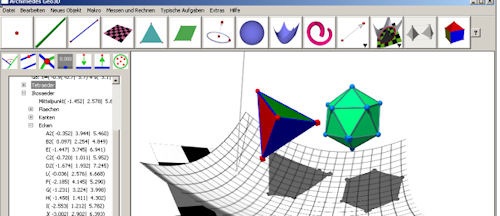 | Archimedes Geo 3D http://www.raumgeometrie.de wurde von dem Göttinger Lehrer Andreas Göbel entwickelt. Er verlangt einen sehr mederaten und gerechtfertigten Sharwarepeis. 
| |||||||
| Kap: Seite 02: S. 1 |
  | Cinderella http://www.cinderella.de/
wurde von den Professoren Jürgen Richter-Gebert und Ulrich Kortenkamp entwickelt. Man kann damit sehr viel wunderbare Mathematik machen. Die Handlungslogik ist aus heutiger Sicht nicht ganz so intuitiv wie die des deutlich jüngeren GeoGebra. Ich verwende Cinderella gerne für Fraktale und ähnich ressourcen-intensive Fragestellungen Auf der Plattform Mathevital stellt Prof. Richter-Gebert erstaunliches und mathematisch verlässliches Material mit Cinderella-Programmen zur Verfügung. Eine Besondertheit ist die Einbindung eine Skriptsprache, die eigenständiges Programmieren erlaubt. | |||||||
| www.kurven-erkunden-und-verstehen.de | ||