|
| 02 Werkzeugkasten |
| Website zum Buch: Hier sind die Dateien, die die Bilder des Buches erzeugt haben, die Aufgabenlösungen, Beweis-Ergänzungen und weitere Kurven, für die im Buch kein Platz mehr war. Wenn Sie hier etwas nicht verstehen, lesen Sie im Buch. Falls Sie Fehler finden ober noch Fragen übrig sind, wenden Sie sich an mich. |
2.1-2.2 Grundlage  | 2.3 Polar
|
2.4 Parametrisch | 2.5 Typen und 3D |
2.7-2.7 GeoGebra u. a. Software  |
 2.1 und 2.2 Kurven in Geometrie und im Koordinatensystem | ||||||
| Kap: Seite 2.2: S. 7 |
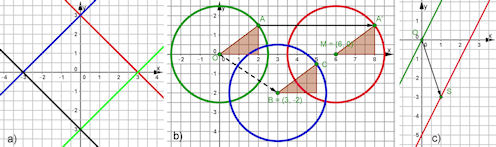 | Abb. 2.1 Gleichungen verstehen: a) implizite Geradengleichungen entdecken, b) Gleichungen für verschobene Kreise, c) Gleichung für eine verschobene Gerade  im GeoGebra-Book
download
Kann man solche Gleichungen nach y auflösen, so ist die explizite Gleichung \(y=f(x)\) i.d.R. eine Funktion. | ||||
| Kap: Seite 2.2.3: S. 9 |
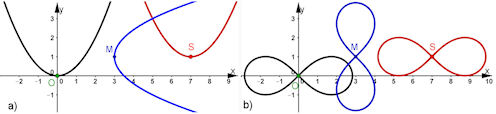 | Abb. 2.2 Kurvengleichungen und Verschiebungen: a) schwarze Parabel \(y-\frac{1}{2}x^2 = 0\), b) schwarze
Lemniskate \((x^2 + y^2)^2 - 2e^2(x^2 - y^2) = 0\). | ||||
| Parabeln download
Lemniskaten im GeoGebra-Book
Lemniskaten download
| ||||||
| Kap. 2.2.3.3 Seite 11 |
| |||||
| 2.3 Was sind Polarkoordinaten? | ||||||
| Kap: Seite 2.3: S. 12 |
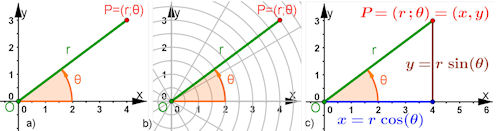 | Abb. 2.3 Polarkoordinaten verstehen: a) Grundaussage, b) Grundaussage im „Polargitter“, c) begründet die Grundgleichungen 2.6 \(x = r(\theta)\cdot cos(\theta)\) \(y = r(\theta)\cdot sin(\theta)\) download
| ||||
| Kap: Seite 2.3: S. 12 |
 | Abb. 2.4 Polarkoordinaten Definition Teil 2: a) Fur negative Polarradien wird \(P_n = (|r|;\theta)\) am Ursprung gespiegelt. b) Die Grundgleichungen 2.6 gelten weiterhin. download
| ||||
| Kap: Seite 2.3.4.1: S. 17 |
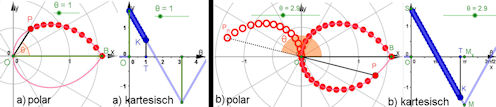
 | Abb. 2.5 Start in die polar-kartesische Darstellung in zwei gekoppelten Grafikfenstern.
a) polar: positiver Radius von \(P = (r(\theta); \theta)\) im Polargitter, a) kartesisch: \(K = (\theta, r(\theta))\) oberhalb der x-Achse, | ||||
| b) polar: \(P = (r(\theta); \theta)\) mit negativem Radius im Polargitter, zusätzlich zeigt der
Fahrstrahl von \(P_n = (|r(\theta)|; \theta)\) den Polarwinkel theta,
b) kartesisch: \(K = (\theta, r(\theta))\) liegt bei diesem
theta unter der x-Achse. Die untere Bildserie zeigt zusammenfassend wie die Bewegungen von \(P\) und \(K\) zusammenhängen. | ||||||
| Kap: Seite 2.3.4.12: S. 17 ergänzt |
 |
Zu Abb.2.5 ergänztpositiv download negativ download
linkes Bild, download
| ||||
| Kap: Seite 2.3.4.2: S. 17 |
 | Abb. 2.6 Gekoppelte polar-kartesische Darstellung einer Kurve:
a) polar: dicke rote Punkte zeigen selbst theta an. a) kartesisch: \(K = (\theta, r(\theta))\) liegt oberhalb der x-Achse, im GeoGebra-Book
download
| ||||
| b) polar: weiter auf
der Kurve mit negativem Radius und dicken roten Punkten im Polargitter, zusätzlich zeigt der
Fahrstrahl von \(P_n\) mit offenen roten Punkten den Polarwinkel \(\theta\),
b) kartesisch: \(K\) ist nun unter die x-Achse gewandert. | ||||||
| 2.4 Was ist eine Parameterdarstellung? | ||||||
| Kap. 2.4.1 Seite 19 |
| |||||
| Kap: Seite 2.4.2: S. 20 |
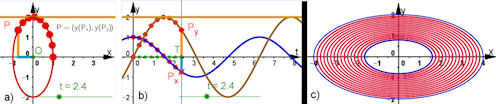 | Abb. 2.7 a) und b) Parameterdarstellung einer Ellipse in gekoppelter doppelt-kartesischer Sicht
Ellipse im GeoGebra-Book
download
Siehe diese Methode auch bei der Neil'schen Parabel | ||||
| Kap: Seite 2.4.2: S. 20 |
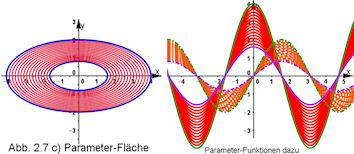 | Abb. 2.7 Parameterdarstellung doppelt-kartesisch
c) Mit zwei Parametern entstehen viele Ellipsen zwischen zwei Ellipsen. So kann gemäß Gleichung 2.9 ein Gebiet in der Ebene dargestellt werden. Parameterfläche im GeoGebra-Book
download
| ||||
| 2.5 und 2.6 Kurventypen und 3D-Raum | ||||||
| Kap: Seite 2.6: S. 27 |
 im GeoGebra-Book
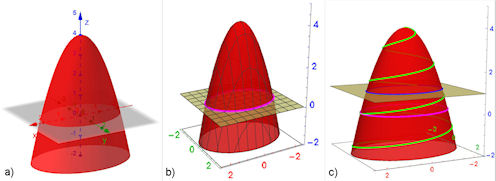download | Abb. 2.8 Paraboloid: a) in GeoGebra 3D, b) Grundebene mit Gitter und violetter Ellipse als Schnittkurve, die Bilder eines Gitters auf der Raumfläche heißen Grids, c) zusätzlich verschobene Ebene mit blauer Schnittellipse und eine grüne Raumkurve auf dem Paraboloid Die Bilder c) und d) sin im Buch und dem gezeigten Bild mit Mathematica gemacht. Inzwischen aber kann das GeoGebra auch(ohne die Grids). Darum hat die hier verfügbare Datei alle in GeoGebra verwirklicht. | ||||
| Kap: Seite 2.6.2.1: S. 29 |
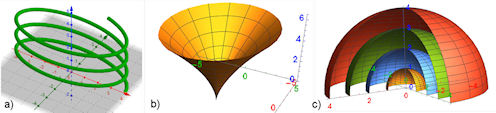 | Abb. 2.9 a) Schraubenlinie als Raumkurve in GeoGebra 3D (s. Abschnitt 2.
Schraubenlinie im GeoGebra-Book
download
6.2.1),
b) Parametrische Raumfläche mit der Neil’schen Parabel in Schnitten, die die z-Achse enthalten, und Ellipsen in Schnitten senkrecht zur z-Achse (s. Abschnitt 2.6.2.2), c) vier Halbkugeln, die zu einem Viertel offen sind, in Kugelkoordinaten (s. Abschnitt 2.6.2.3)  Mathematica-Notebook für b) und c)
Zum Lesen in pdf
| ||||
| Kap: Seite 2.6.2.3: S. 30 |
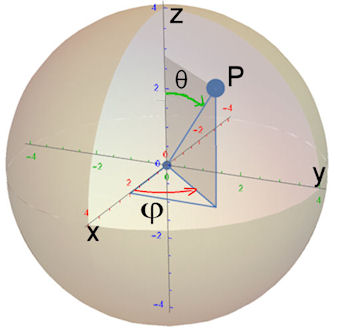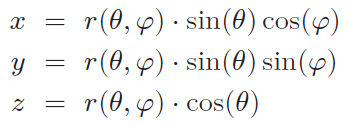  | Abb. 2.10 Kugelkoordinaten, sphärische Koordinaten
Der Punkt \(P = (x, y, z)\) habe den Abstand |r| vom Ursprung. Der Polarradius \(r\) ergibt sich als Funktion zweier Winkel \(\theta\) und \(\varphi\) zu \(r = r(\theta, \varphi)\). Die Winkel werden in nebenstehender Weise gemessen. Die 3D-Parameterdarstellung ist links gezeigt. Mathematica-Notebook für b) und c)
Zum Lesen in pdf
| ||||
| Varianten der Kugelkoordinaten In der Geografie und in GPS-Systemen werden Kugelkoordinaten
mit etwas anders definierten oder benannten Winkeln verwendet. Wenn
die Erde näherungsweise als Kugel angesehen wird, durchstößt die z-Achse die Erde am
Nord- und Südpol, der halbe Großkreis, der durch die positive x-Achse verläuft, ist der
"Nullmeridian von Greenwich"g. Der Winkel, der in Abb. 2.10 \(\varphi\) heißt, wird \(\lambda\)
genannt. Er wird "östlich"(+) und "westlich" (-) mit Gradzahlen bis 180° gemessen.
Entsprechend heißen auch Meridiane. ....mehr im Buch...
Die wirklichen GPS (Geo-Positioning-System) betrachten die Erde als Ellipsoid, aber auch das ist nur näherungsweise richtig. Lesen Sie in Wikipedia über GPS. Die Definition von Kugelkoordinaten in Abb. 2.10 entspricht dem internationalen Gebrauch in der Physik. | ||||||
 | Sie finden Weiteres zu Kurven auf meiner Site www.mathematik-verstehen.de im Bereich Kurven | |||||
 Prof. Dr. Dörte Haftendorn |
Erstellt August 2016, Update |
www.kurven-erkunden-und-verstehen.de |
| ||