|
04 Barocke Blüten und Früchte 
4.2 Neil'sche Parabel und andere Kubiken |
| Website zum Buch: Hier sind die Dateien, die die Bilder des Buches erzeugt haben, die Aufgabenlösungen, Beweis-Ergänzungen und weitere Kurven, für die im Buch kein Platz mehr war. Wenn Sie hier etwas nicht verstehen, lesen Sie im Buch. Falls Sie Fehler finden ober noch Fragen übrig sind, wenden Sie sich an mich. |
4.1 Versiera  | 4.2 Kubiken  |
4.3 Cassini u.a.bipolare Kurven | 4.4.1 und 4.4.2 Lemniskate |  BMG-Lemniskate Zusatz |
4.4.3-4.4.7 Gelenke |
| Kap: Seite 4.2: S. 91 |
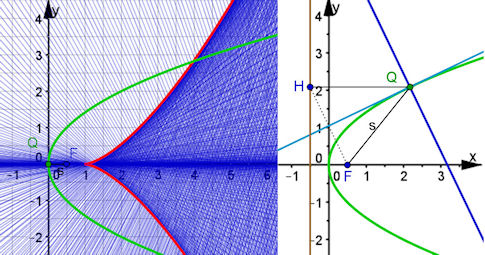 | Abb. 4.10 Tangenten und
Normalen für die Parabel:
Fälle von Q das Lot auf die Leitgerade. Der Fußpunkt sei H. Die Mittelsenkrechte von FH ist die Tangente in Q. Die Senkrechte auf der Tangente in Q ist die Normale. Ziehe Q und lasse die Normale ihre Spur zeichnen. Es entsteht die Neil’sche Parabel als Hüllkurve.  im GeoGebra-Book
download
|
| Kap: Seite 4.2: S. 91 ergänzt |
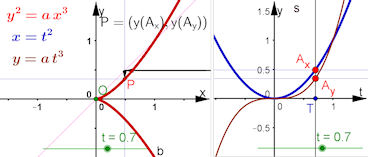 | Parameterdarstellung der Neil'schen Parabel in doppelt-kartesischer Sicht.
im GeoGebra-Book
download
|
| Kap: Seite 4.2 : S. 93 |
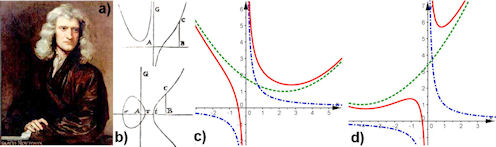 | Abb. 4.11 Newton und die Kubiken Gruppe II: a) Newton-Portrait von G.Kÿ neller 1669, b) Kubiken von Newton selbst, c) und d) Parabel + Hyberbel = Kubik im GeoGebra-Book
download
|
| Kap: Seite 4.2.2.3: S. 95 |
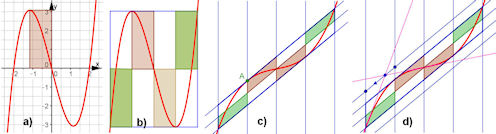 | Abb. 4.12 Polynome im Affenkasten: a) Ein Extrempunkt und der Wendepunkt definieren ein Rechteck. b) In den Affenkasten aus acht solchen Rechtecken passt stets das Polynom in gezeigter Weise. c) Dieses gilt entsprechend für jeden Punkt A und seine Tangente. d) Die Wendetangente und die Tangente in der äußeren Kastenecke treffen sich auf dem Doppelkasten an einem Drittelpunkt einer Kastenzelle. im GeoGebra-Book
download
|
| Kap: Seite 4.2.2.4: S. 97 |
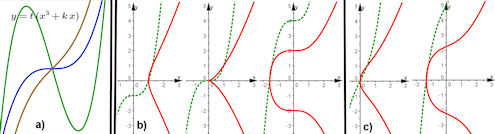 | Abb. 4.13 Kubiken: a) vom IV.Typ , b), c) vom III.Typ mit k >=0: b) Kubik zu p3(x) = x^3, k = 0 Sattelfunktion verschoben, c) Kubik zu p3 mit k > 0 im GeoGebra-Book
download
|
| Kap: Seite 4.2.2.4: S. 97 |
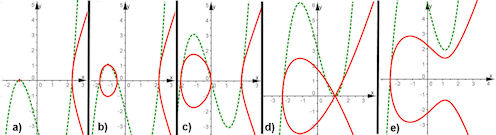 | Abb. 4.14 Kubiken vom III. Typ mit k < 0, also hat p3 zwei Extrema: a) isolierter Punkt b)
und c) Oval und Bogen d) Newton’scher Knoten e) „Knauf“
Dateien beim vorigen Bild |
| Kap: Seite 4.2.2.5: S. 98 |
 | Abb. 4.15 Vier Kubiken vom I. Typ: Trisektrix, Cissoide, Versiera, Strophoide. Kubik vom III. Typ: Neil’sche Parabel im GeoGebra-Book
download
|
 Prof. Dr. Dörte Haftendorn |
 Erstellt August 2016, Update |
www.kurven-erkunden-und-verstehen.de |
| ||