|
03 Klassische Kurven ohne Ende 
3.4 Cissoiden, die Efeukurve und ihre Verwandten |
| Website zum Buch: Hier sind die Dateien, die die Bilder des Buches erzeugt haben, die Aufgabenlösungen, Beweis-Ergänzungen und weitere Kurven, für die im Buch kein Platz mehr war. Wenn Sie hier etwas nicht verstehen, lesen Sie im Buch. Falls Sie Fehler finden ober noch Fragen übrig sind, wenden Sie sich an mich. |
3.1 Konchoiden  |
3.2 Strophoiden | 3.3 Cissoiden  |
3.4 Trisektrix  | 3.5 Analysis hierbei |
| Kap. 3.4.2: Seite 67 Allgemeine Definition der Cissoide im Vergleich mit den anderen allgemeinen Definitionen
| ||
Allgemeine  Lernseite  Cissoide  | ||
| Kap: Seite 3.4.1: S. 65 |
 |
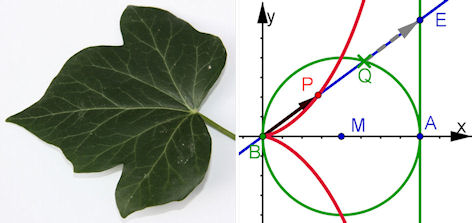Abb. 3.19 Efeukurve:
Zeichne B = (0, 0), den Kreis um M = (a, 0) mit Radius a und die Senkrechte g auf BA in A = (2a, 0). Setze Q zugfest auf den Kreis und zeichne die Gerade BQ. Die Gerade BQ schneidet die Senkrechte g in E. Der Vektorpfeil ¨ QE wird an B angehängt und ergibt dadurch den Punkt P.  im GeoGebra-Book
download
|
| Kap: Seite 3.4.1.1: S. 65 Kap: Seite 3.4.1.3: S. 66 |
  |
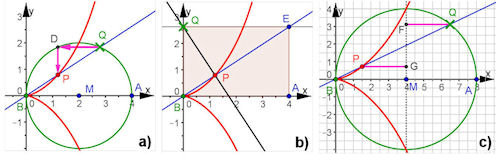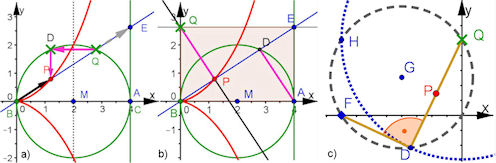Abb. 3.20 Weitere Konstruktionen für die Cissoide in a) und b) und eine Rasterkonstruktion in c). Konstruktionsbeschreibungen kann man "sehen". Darunter Abb. 3.21 Cissoide: a) und b) Beweiselemente zu obigen Konstruktionen in Abb. 3.20 a) und b), in c) finden Sie eine vierte Konstruktion. Konstruktion a)
Konstruktion b)
Konstruktion c)
Konstruktion Abb. 3.21c)
|
Allgemeine Definition der Cissoide | ||
| Kap. 3.4.2, Seite S. 67 Abb. 3.22 Allgemeine Definition der Cissoide im Vergleich mit den anderen allgemeinen Definitionen | ||
| Kap: Seite 3.4.3.2: S. 69 |
 |
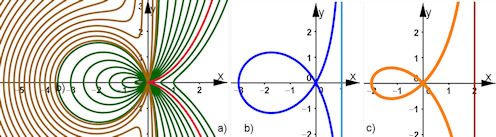Abb. 3.23 Cissoiden nach Gl. 3.16 mit a = 2:
a) braun -2.6<= c<<=0.4, Schrittweite = 0.2, grün 0.5 <=c <= 5, Schrittweite = 0.5 und rot c = 4, die Cissoide des Diokles, b) c = 1 Trisektrix. c) c = 2 Strophoide im GeoGebra-Book
download
|
| Kap: Seite 3.4.4.2: S. 70 |
 |
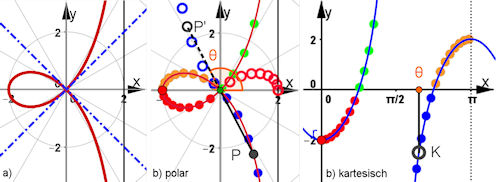Abb. 3.24 Strophoide mit Doppelpunkt im Ursprung und polar-kartesischer Darstellung, anders
als Abb. 3.11
im GeoGebra-Book
download
|
| Kap: Seite 3.4.5: S. 71 |
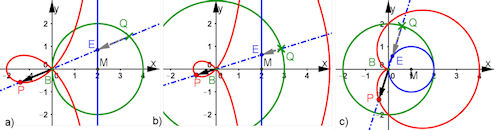 Strophoide als Cissoide nach Gl. 3.19 download Konchoide als Cissoide download Pascal'sche Schnecke als Cissoide download | Abb. 3.25 Geometrische Konstruktion mit dem Cissoiden-Prinzip, Grundlage ist die als Cissoide gedeutete Polargleichung, a) Strophoide, b) Konchoide des Nikomedes, c) Kardioide als spezielle Pascal’sche Schnecke |
| Kap: Seite 3.4.5: S. 73 |
a) Top 1., downl.
b)Top 2., downl.
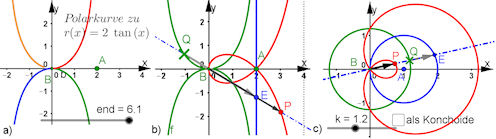
c) Top 4., downl. Aufgabe 3.7 Umfeld der Cissoiden Top 3., download Top 5., download | Aufgabe 3.7 Umfeld der Cissoiden a) Top 1., Polarkurve zum Tangens, b) Top 2., Geometrie einer neuen Konstruktion der Strophoide durch Deutung der Polargleichung als Cissoide c) Top 4., Geometrie einer neuen Konstruktion der Pascal'schen Schnecke mit Schlaufe durch Deutung der Polargleichung als Cissoide. |
| Kap: Seite 3.4.6: S. 73 |
download (wie links)
download (vollständig) |
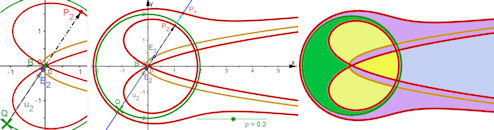
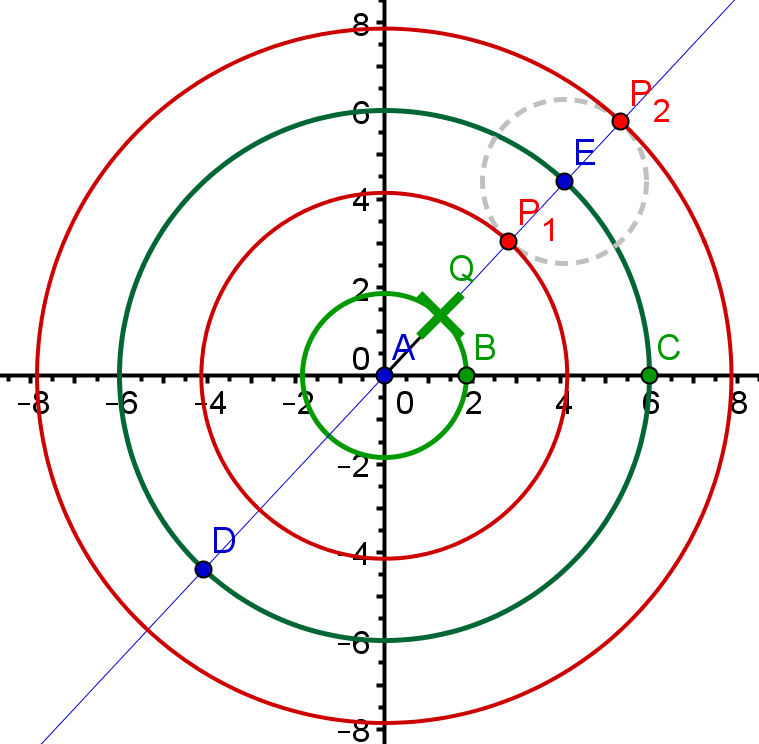
Abb. 3.26 Cissoide bezüglich Kreis (grün) rho1(theta)=a für a = 2 und Parabel (gelb). Die Parabel hat ihren Brennpunkt im Ursprung und die Gleichung 7.4: rho2(theta)= p/( 1-cos(theta)) für p = 0.2. Links sehen Sie im Ausschnitt die Konstruktion von P2: Der Vektor QE wird an B angehängt, um P zu erzeugen. |
| Kap: Seite 3.4.6: S. 74 |
Ellipse-Hyperbel, download
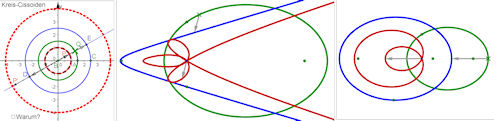
Ellipse-Ellipse, downloadAufgabe3.8 Cissoiden der Kegelschnitte | Aufgabe 3.8 Cissoiden der Kegelschnitte Links zu Frage c) Datei siehe Abb. 3.26 oben, Mitte und rechts zu b): Die Kegelschnitte sind jeder aus zwei auf die x-Achse gesetzten Brennpunkten und einem weiteren Punkt entstanden. Obwohl die Bilder reduziert sind, können Sie die Konstruktion sehen. Der kleine blaue Punkt ist der Ursprung, das grüne Kreuz ist Q. Man kann es aber auch ganz anders machen. |
Das Folgende sind ältere Vesionen, ich brauche sie noch, wenn ich die Aufgabenlösungen mache. | ||
| Vorbereitung | cissoide-definitionKr-Gr |
 |
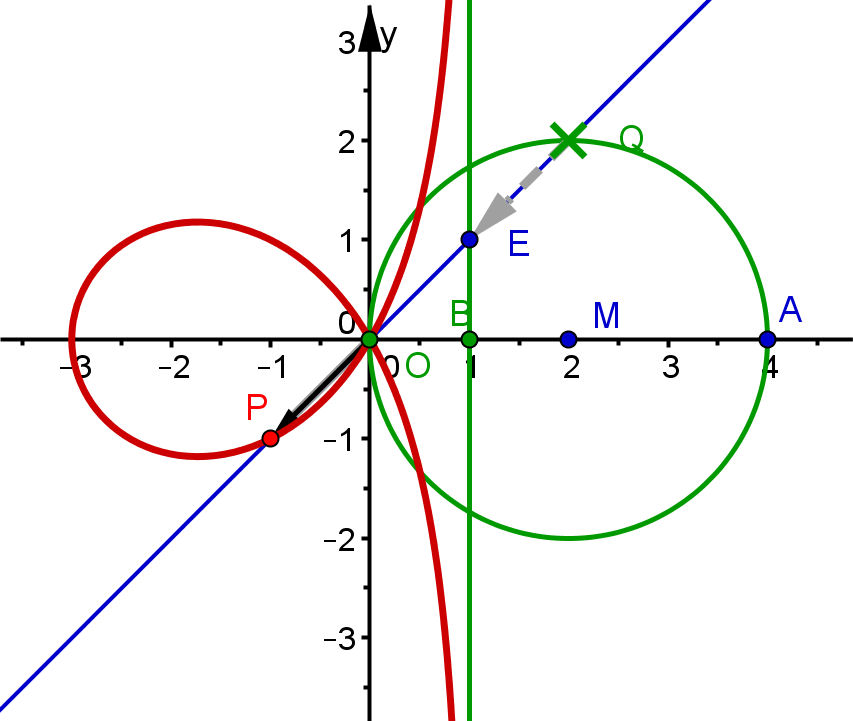| cissoide-herzchen |
 |
|
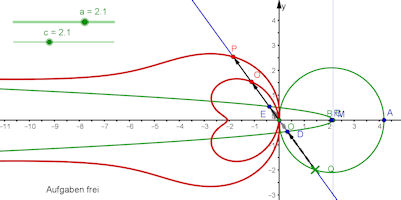| Cissoide-Ursprung |
 |
|
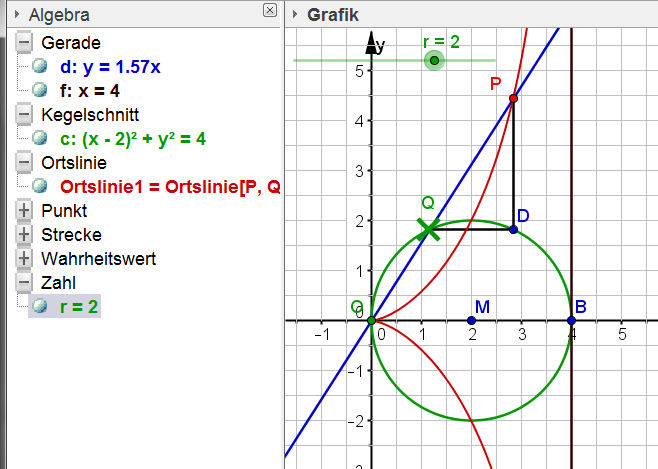| cissoide-3d.ggb unbefriedigend |
||
| Cissoide-Ursprung+deli.ggb |
||
| Cissoide-trivial.ggb |
 |
|
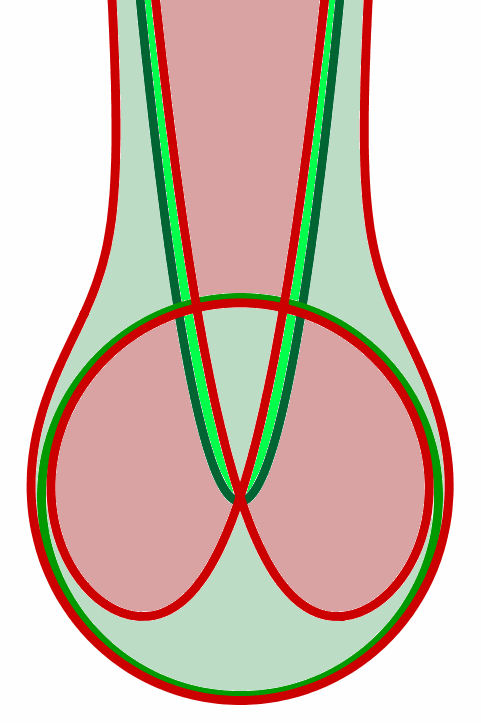
| Cissoide-trivial-parabel-pur.ggb |
 |
|
| |
||
| Cissoide-Fusspkt.ggb |
||
| CissoideAllgemein.ggb |
 |
|
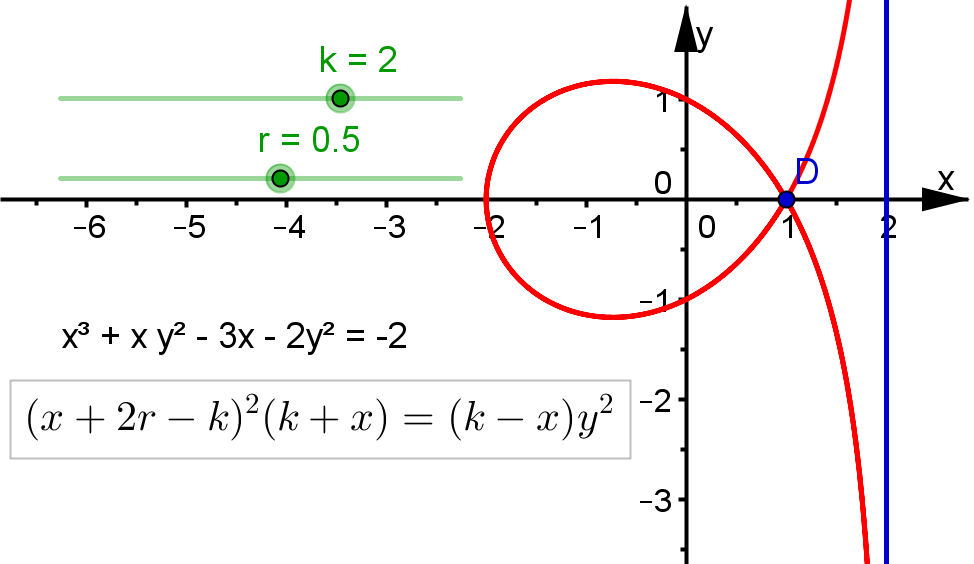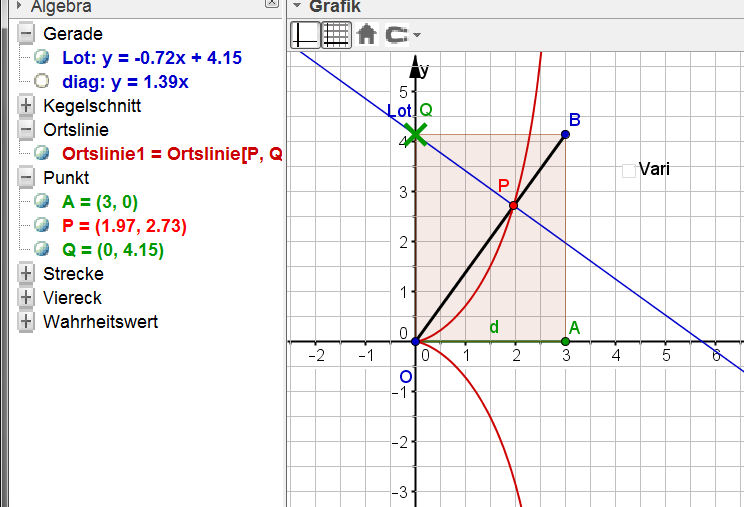
| Cissoide-Draeger11.ggb |
 |
|
| |
||
| Cissoide-BK-13d.ggb |
 |
|
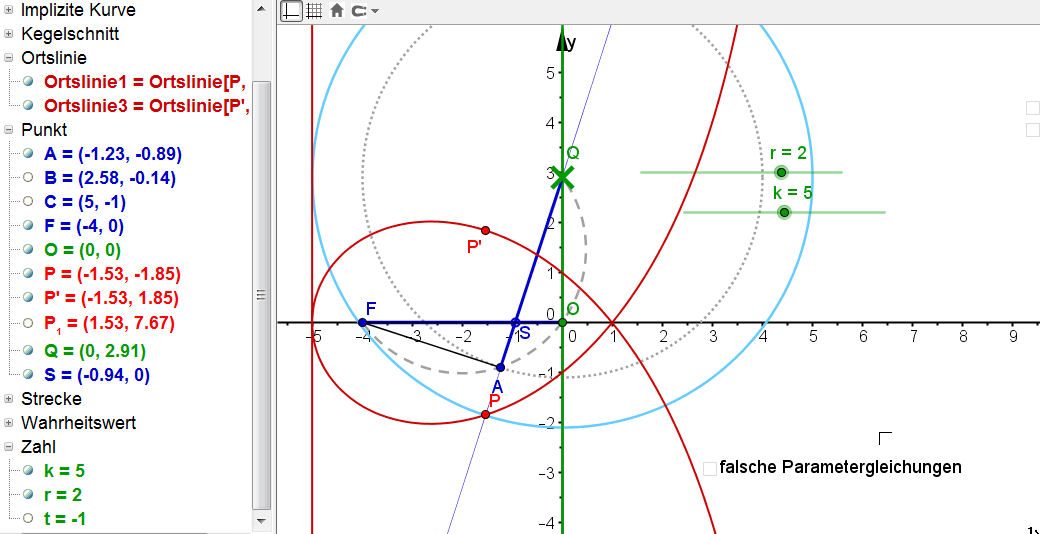| Cissoide-BK-13c.ggb |
 |
|
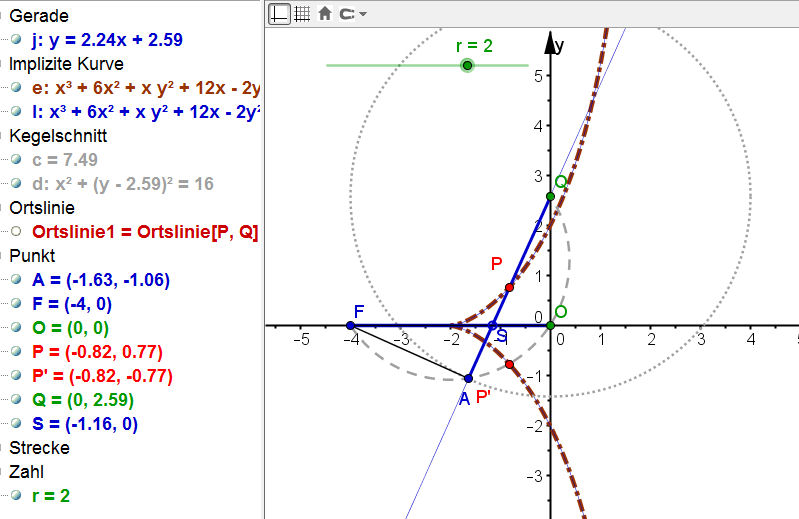| Cissoide-Wieleitner50.ggb |
  |
|
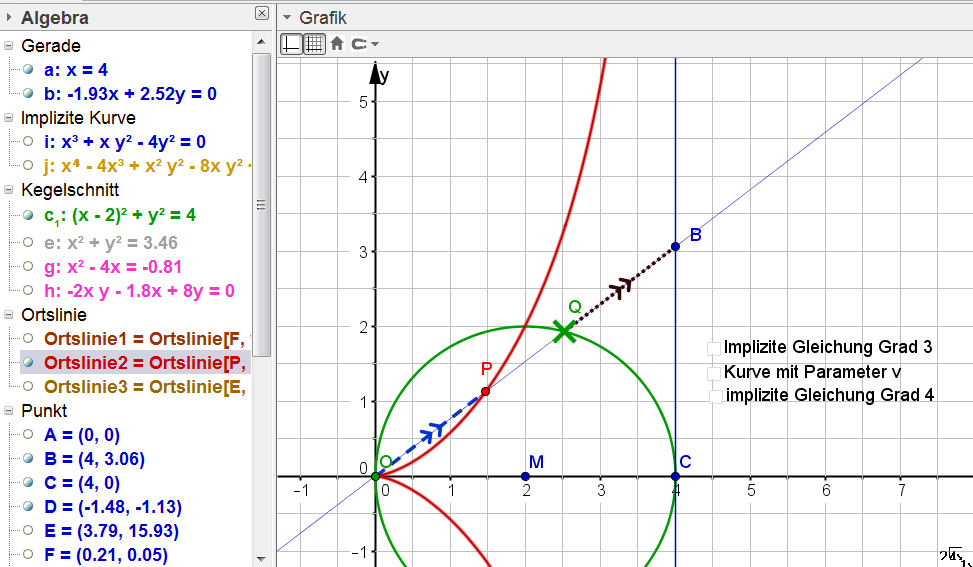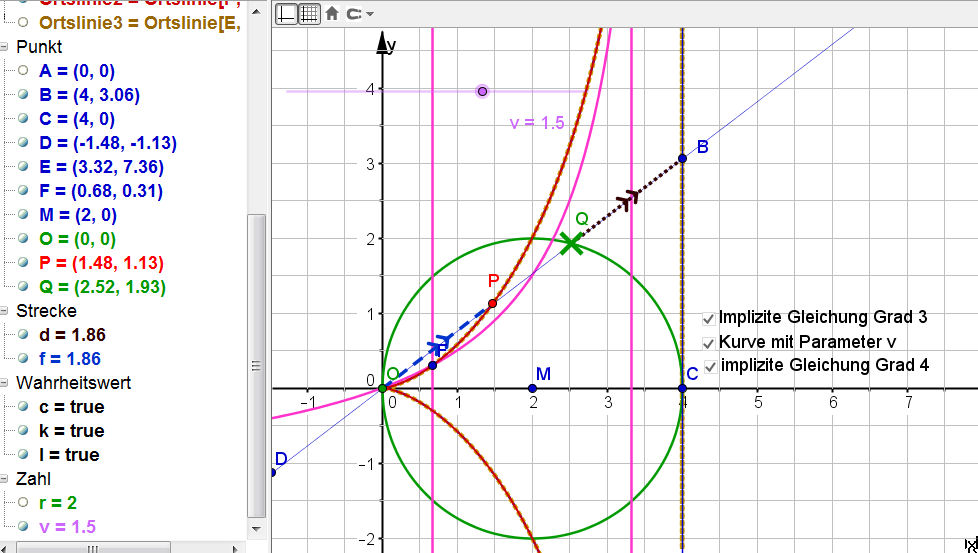| Cissoide-BK-13b.ggb |
||
| Cissoide-BK-13a.ggb |
||
| Cissoide-BK-12.ggb |
||
| |
||
| |
||
| |
||
| |
||
Inhalt und Web:  Prof. Dr. Dörte Haftendorn |
 August 2016, Update |
www.kurven-erkunden-und-verstehen.de |
| ||