Konchoiden

03 Klassische Kurven ohne Ende

3.1 Konchoiden, die Hundekurve und Ihre Verwandten

Website zum Buch: Hier sind die Dateien, die die Bilder des Buches erzeugt haben, die Aufgabenlösungen, Beweis-Ergänzungen und weitere Kurven, für die im Buch kein Platz mehr war. Wenn Sie hier etwas nicht verstehen, lesen Sie im Buch. Falls Sie Fehler finden ober noch Fragen übrig sind, wenden Sie sich an mich.

Kap. 3.1.2: Seite 43 Allgemeine Definition der Konchoide im Vergleich mit den anderen allgemeinen Definitionen
	Allgemeine Lernseite Konchoide darin Abb. 3.1 und Abb.3.3
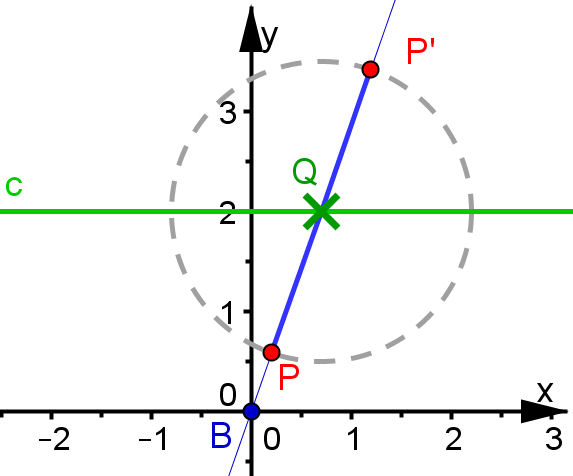Kap: Seite 3.1.1: S. 38		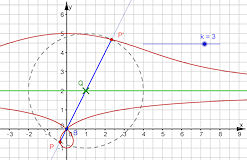Abb. 3.2 Konstruktion der Hundekurve Setze B = (0, 0) und zwei Konstanten a und k als Schieberegler. Setze y = a (Gerade als Straße) und darauf Q zugfest. Erzeuge die Gerade g = BQ und schneide sie mit dem Kreis um Q mit dem Radius k. Zeichne die Ortslinien von P und P' bezüglich Q. Konstruktion pur Hundekurve im GeoGebra-Book Hundekurve download
	Aufgabe 3.1 Visuelles Prüfen von Termumformungen Aufgabe 3.1 zu den Termen Grundlegendes zu Termen und Gleichungen auf der Site www.mathematik-verstehen.de
Kap: Seite 3.1.3: S. 45		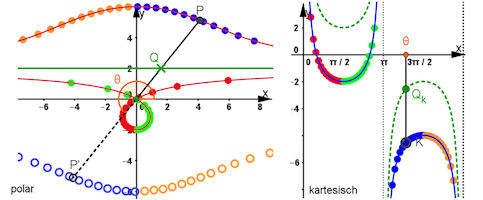Abb. 3.4 Abb. 3.4 Polar-kartesische Darstellung der Konchoide des Nikomedes (Hundekurve). Wenn theta von 0 bis 2 pi läuft, werden nacheinander rote, grüune, blaue und gelbe dicke Punkte gezeichnet. Die offenen violetten, blauen und gelben Punkte sind die Hilfspunkte, die wegen der negativen Radien entstehen. im GeoGebra-Book download

Kap: Seite 3.1.4: S. 46	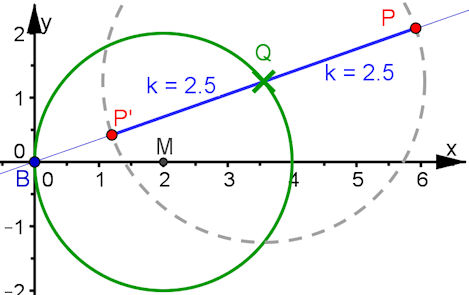Abb. 3.5 Konstruktion der Pascal'schen Schnecken Setze B = (0, 0) und zwei Konstanten a und k als Schieberegler. Schlage einen Kreis um M = (a, 0) mit dem Radius a. Setze darauf Q zugfest. Erzeuge die Gerade g = BQ und schneide sie mit dem Kreis um Q mit dem Radius k. Zeichne die Ortslinien von P und P' bezüglich Q. Variation: B = (b, 0) mit b <0.	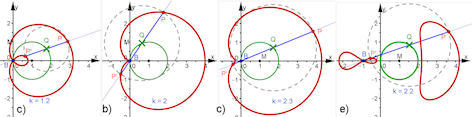Abb. 3.6 Pascal’sche Schnecken, Wanderkreis-Radius a, Leine k a) Schlaufe für k < 2a, b) Kardioide (mit Spitze) für k = 2a und c) nur Einbuchtung für k > 2a. In d) wurde die Baumstellung variiert. Abb.3.6 im GeoGebra-Book Abb.3.6 download 3.2 Erkundung Pascal'scher Schnecken Aufgabe 3.2 Pascal polar-kartesisch Aufgabe 3.2 Pascal'sche Schnecken und ihre Verwandten, Sonderfall mit zwei Kreisen

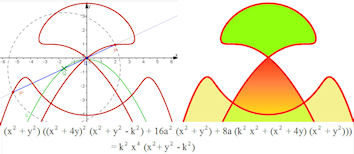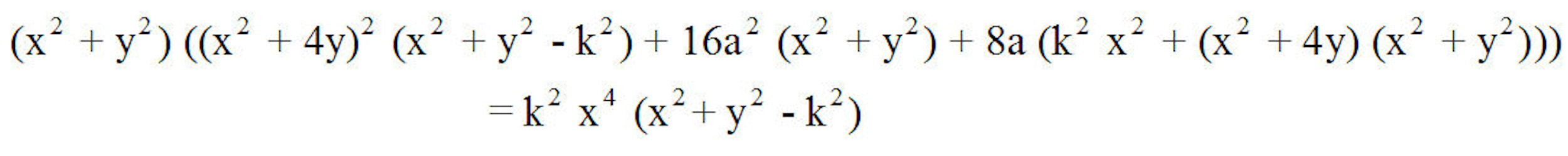
Kap: Seite 3.1.5: S. 49		Abb. 3.7 Konstruktion der Konchoide der Parabel y = -1/4 x^2 - a mit a = 0.1, dem Baum im Ursprung und der Leinenlänge k = 4. Die Formel hat a und k als Parameter. Diese Parabel-Konchoide ziert das Cover. Cover-Kurve im GeoGebra-Book Cover-Kurve download
Nach der Gleichung Cover-kurve-Beweis in Mathematica Aufgabe 3.3 Formenreichtung und Coverkurve
Kap: Seite 5.1.1: S.134 1: S.1	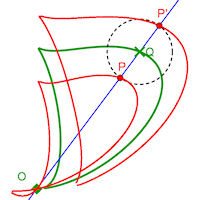Konchoiden kann man zu jeder Kurve konstruieren. Die allgemeine Definition ist auf der Seite "klassische Kurven". Wenn die Leinenlänge klein ist gegenüber den Abmessungen der Kurve, erhält man, wie hier zu sehen ist, eine Form, die man auch "zentrisch parallel" nennen könnte. Bei echten Parallelkurven wird der stets gleiche Abstand auf der Normalen abgetragen. Siehe im Buch Seite 273.	Abb. 5.1 D-Kurve und ihre Konchoide mit dem Baum in B. Mehr zur D-Kurve im GeoGebra-Book download

Kap: Seite 3.1.5: S. 49		Abb. 3.8 Allgemeine Konchoiden als Anregungen zu Aufgabe 3.3 a) einer Parabel, b) einer Kosinuskurve, c) einer variierten Sinuskurve Sinuskonchoide im GeoGebra-Book
	a) Parabel download b) Kosinus download c) Sinus download
	Zurück zur Ableitung von Kurven auf "Höhere Mathematik sehen und verstehen"