03 Klassische Kurven ohne Ende 3.2 Strophoiden: die Seilkurve und ihre Verwandten

Website zum Buch: Hier sind die Dateien, die die Bilder des Buches erzeugt haben, die Aufgabenlösungen, Beweis-Ergänzungen und weitere Kurven, für die im Buch kein Platz mehr war. Wenn Sie hier etwas nicht verstehen, lesen Sie im Buch. Falls Sie Fehler finden ober noch Fragen übrig sind, wenden Sie sich an mich.

3.1 Konchoiden

3.2 Strophoiden

3.3 Cissoiden

3.4 Trisektrix

3.5 Analysis hierbei

Kap. 3.2.2, Seite S. 58   Allgemeine Definition der Strophoide im Vergleich mit den anderen allgemeinen Definitionen
	Allgemeine Lernseite zur Strophoide
	Kurven mit Ti Nspire am Beispiel der StrophoideLernseite zur Strophoide    Handzettel     download
Kap: Seite 3.2.1: S. 50		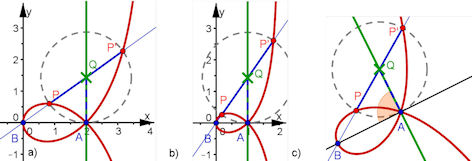Abb. 3.10 Gerade Strophoiden: a) und b) unterscheiden sich lediglich durch den Maßstab, der durch die Abszisse a von A gesteuert wird. c) zeigt die rein geometrische Auffassung der Konstruktionsbeschreibung ohne ein Koordinatensystem. Wegen des rechten Winkels bei A ist die Kurve auch eine gerade Strophoide. im GeoGebra-Book    download
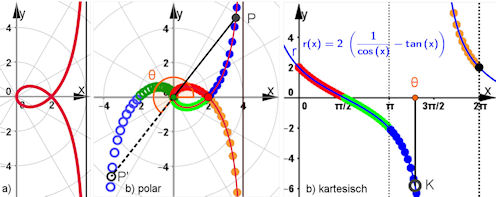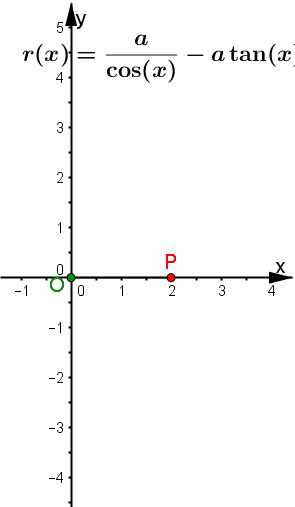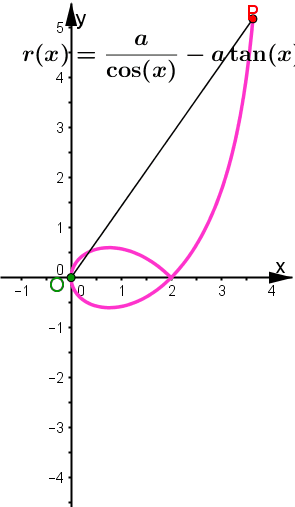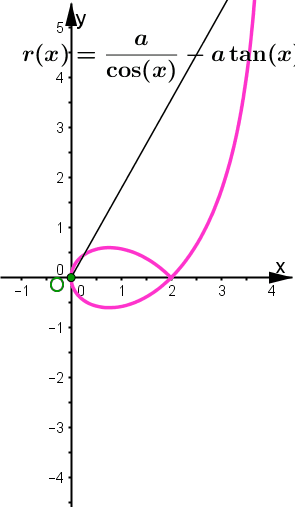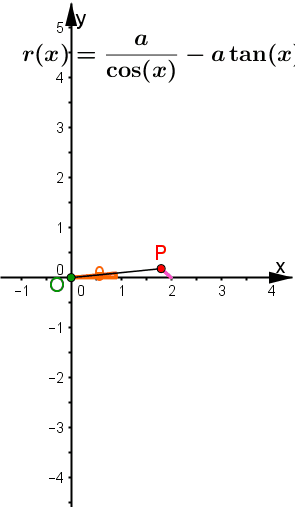
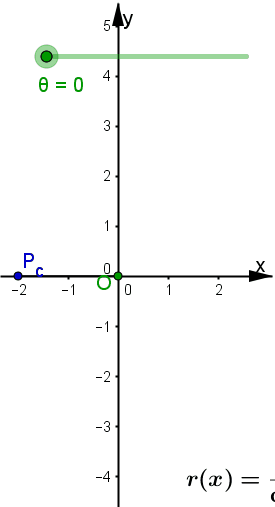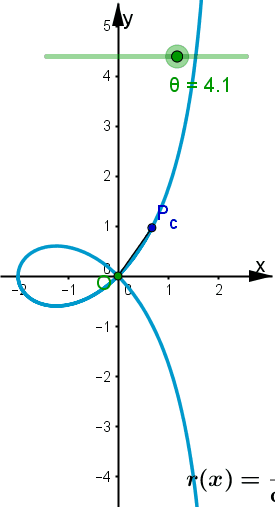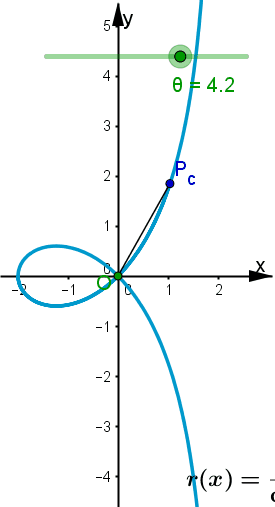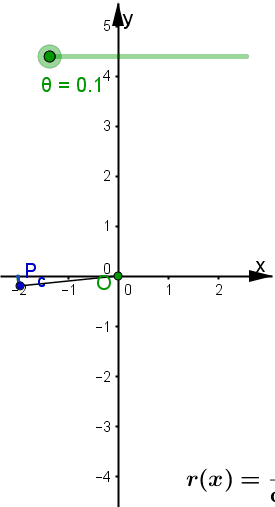
Kap: Seite 3.2.1.5: S. 53		Abb. 3.11 Polar-kartesische Darstellung der geraden Strophoide: a) Strophoide im Polargitter, b) gekoppelte Grafikfenster in GeoGebra, für von 0 bis 2pi wachsendes theta werden nacheinander die ausgefüllten roten, grünen, blauen und gelben Punkte durchlaufen. Die offenen grünen und blauen Punkte sind die Hilfspunkte, die für negative Radien entstehen. Letztere sind rechts durch die grünen und blauen Punkte unterhalb der x-Achse angezeigt. im GeoGebra-Book    download Siehe auch Abb. 3.24
Kap: Seite 3.2.1.7: S. 55		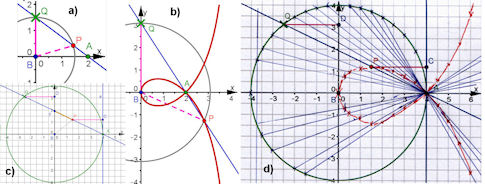Abb. 3.12 a) und b) Logocyclica, c) und d) Konstruktion und ihre punktweise Durchführung für die Rasterschlaufe, siehe Abschnitt 3.2.1.8. Rasterschlaufe
Kap: Seite 3.2.1.7: S. 55		Logocyclica eine lohnende Variante, mit geometrischem Beweis Logozyklika download Logocyclica-Beweis Beweis download
Kap: Seite 3.2.1.9: S. 57		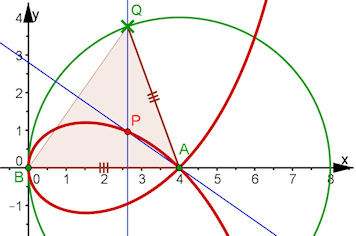Abb. 3.13 Höhenschnittpunkt im Dreieck Setze die Punkte B = (0, 0) und A(a, 0) mit beliebigem a. Schlage um A einen Kreis mit dem Radius BA und setze darauf Q zugfest. Zeichne das Dreieck BAQ und konstruiere zu ihm zwei Höhengeraden. Gesucht ist die Ortslinie des Höhenschnittpunktes P, wenn Q auf dem Kreis wandert. Aufageb 3.4 Der Höhenschnittpunkt wandert. im GeoGebra-Book    Grundbild download mit Beweiselementen download
Kap: Seite 3.4.4.2: S. 70		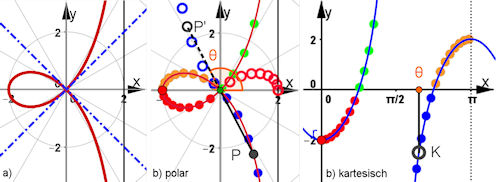Abb. 3.24 Strophoide mit Doppelpunkt im Ursprung und polar-kartesischer Darstellung, anders als Abb. 3.11 im GeoGebra-Book    download
Kap: Seite 3.1.3: S. 44		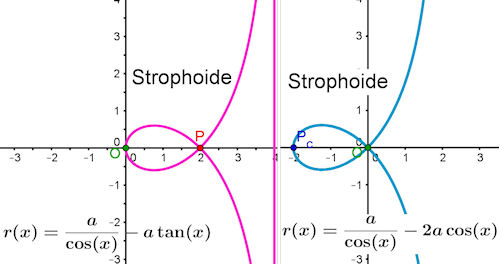Strophoiden im Vergleich,Scheitellage vs. Knotenlage Datei für Vorträge geeignet im GeoGebra-Book    Datei mit allen Strophoiden-Versionen, auch der Inversion zum Auswählen in polar-kartesischer Darstellung (ohne "Punkte") download
Kap: Seite 02: S. 1		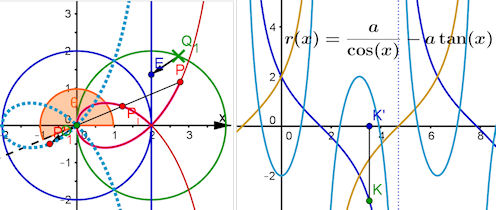Strophoide, drei Polarkurven-drei Duchlauftypen zum Auswählen im GeoGebra-Book    download
Allgemeine Definition der Strophoide
Kap. 3.2.2, Seite S. 58    Allgemeine Definition der Strophoide im Vergleich mit den anderen allgemeinen Definitionen
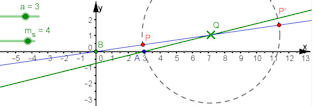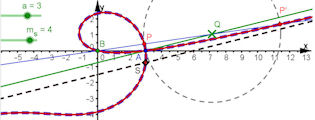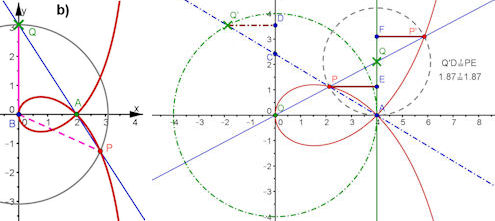
Kap: Seite 3.2.3: S. 59		Abb. 3.14 Schiefe Strophoide: Konstruktion mit Gerade x = k y + a und ms = k, rechts mit Ortslinie und Asymptote. Gestrichelt unterlegt ist die visualisierte Gleichung. download Lernseite zur schiefen Strophoide
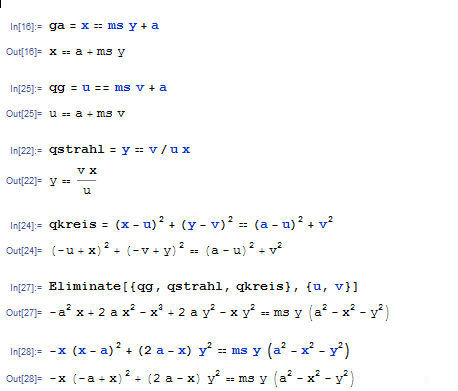		Herleitung der Gleichung der schiefen Strophoide mit Mathematica. Dort werden Gleichungen mit dem Doppelgleichzeichen geschrieben, ihnen kann dann mit dem einfachen Gleichzeichen ein Name zugewiesen werden. ms ist der negative Kehrwert der üblichen Steigung. So kann man erreichen, dass die gerade Strophoide als Sonderfall mit ms=0 dabei ist. Fehlerteufel im Buch Seite 58 Es muss heißen: Eliminate[{u=k v + a, statt Eliminininate[{x=k v + a, Links steht die Berechnung in Mathematica. Im Vergleich gilt: ms=k. (Dort ist alles richtig.)
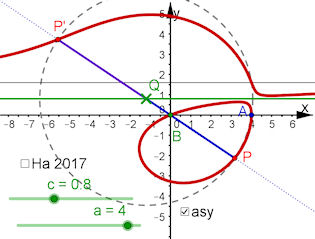
Kap: Seite 3.2.3: S. 60 Aufgabe 3.5	download Aufgabentext 3.5 und Lösung	Zu Aufgabe3.5 Strophoide zu einer waagerechten Geraden Setze die Gerade y=c und die Punkte B=(0,0) und A(a,0) mit beliebigen c und a.\\Setze Q zugfest auf die Gerade und schlage um Q einen Kreis mit dem Radius QA. Die Schnittpunkte der Geraden BQ und des Kreises sind die gesuchten Punkte P und P'. Deren Ortskurve ist die gesuchte Strophoide.
Kap: Seite 3.2.4: S. 61		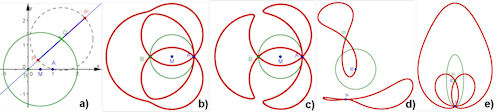Abb. 3.15 Strophoide zu Kreisen: a) Konstruktion, in b)-d) werden die Lage des Mittelpunktes und der Kreisradius variiert, in e) ist die Wanderkurve eine Ellipse
Kap: Seite 3.2.4: S. 61		Aufgabe 3.6 Kreis-Strophoiden
	Kreis-Strophoide    Strophoide frei    Sonderfall    Ellipsen-Strophoide

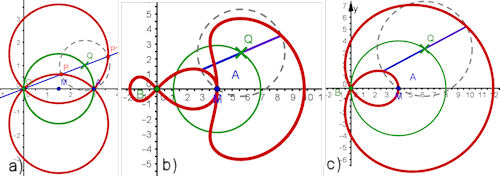Inhalt und Web:  Prof. Dr. Dörte Haftendorn	August 2016, Update 14.02.2021	www.kurven-erkunden-und-verstehen.de