|
| 04 Barocke Blüten und Früchte |
| Website zum Buch: Hier sind die Dateien, die die Bilder des Buches erzeugt haben, die Aufgabenlösungen, Beweis-Ergänzungen und weitere Kurven, für die im Buch kein Platz mehr war. Wenn Sie hier etwas nicht verstehen, lesen Sie im Buch. Falls Sie Fehler finden ober noch Fragen übrig sind, wenden Sie sich an mich. |
4.1 Versiera  | 4.2 Kubiken |
4.3 Cassini u.a.bipolare Kurven | 4.4.1 und 4.4.2 Lemniskate |  BMG-Lemniskate Zusatz |
4.4.3-4.4.7 Gelenke |
 Übersicht über die sechs Themen mit eigenen Leitseiten | |||
| Kap: Seite 4.1: S. 79 |
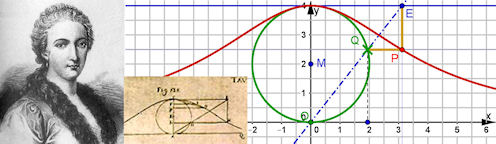
In der Barockzeit war die Beschäftigung mit Kurven "höchst modern". Die mathematische Hilfsmittel waren durch die Verfübarkeit algebraischer Beschreibungen im kartesischen Koordinatensystem teils schon recht weit entwickelt und wurden gerade durch die Beschäftigung mit den Kurven weiter ausgebaut. | 4.1 Versiera Mit Maria Agnesi habe ich das Unterkapitel zur den barocken Kurven eingeleitet. Im Buch steht Einiges über sie. | |
| Kap: Seite 4.2: S. 91 |
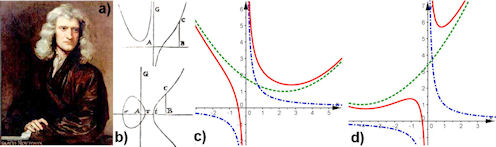 | 4.2 Kubiken Der große Mathematiker und Physiker Isaac Newton untersuchte die Kubiken, also die Kurven 3. Grades sehr systematisch. In diesem Unterkapitel zeige ich sein Vorgehen mit heute modernen Auffassungen und Werkzeugen. Dieses schließt auch besonders gut anschulische Erfahrungen mit Polynomen 3. Grades an. | |
| Kap: Seite 4.3: S. 99 |
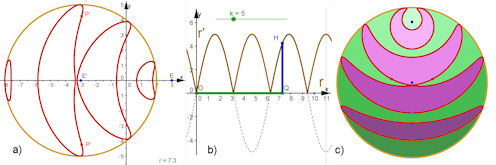 | 4.3 Cassini'sche u.a. bipolare Kurven Die Konstruktion der Bipolaren Kurven ist besonders einfach zu realisieren und eröffnet viele kreative Möglichkeiten. Die Cassini'schen Kurven sind - abgesehen von Ellipsen und Hyperbeln - die bekanntesten bipolaren Kurven. | |
| Kap: Seite 4.4.1+4.4.2: S. 108 |
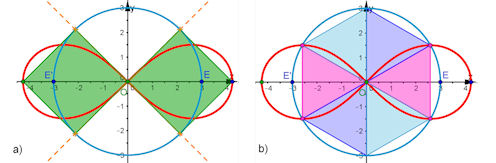 | 4.4.1 und 4.4.2 Lemniskate Die Lemniskate von Bernoulli ist wohl eine der bekanntesten Kurven überhaupt. Die Grundform ist archaisch und kommt in frühesten Kunstwerken der Menschheit vor. Uns ist sie auch vom Unendlich-Zeichen bekannt. | |
| Kap: Seite Nach 4.4.2: S. 117f |
 
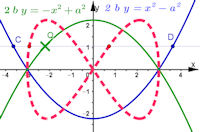
| Nach 4.4.2 BMG-Lemniskate, allg. Gerono'sche Lemniskaten Fünf ausführliche Konstruktionen und ihre Beweise. | |
| Kap: Seite 4.4.3-: S. 119 |
 | 4.4.3-4.4.7 Gelenke Die Mathematiker der Barockzeit haben allerei Stangengelenke erfunden, um Kurven zu zeichnen. Es ging in der Folgezeit aber auch um die mechanische Bewegung von Maschinen, Musikautomaten, Bewegungsspiele und vieles mehr. | |
 Prof. Dr. Dörte Haftendorn |
Erstellt August 2016, Update |
www.kurven-erkunden-und-verstehen.de |
| ||