04 Barocke Blüten und Früchte 4.3 Cassini'sche Kurven und andere bipolare Kurven

Website zum Buch: Hier sind die Dateien, die die Bilder des Buches erzeugt haben, die Aufgabenlösungen, Beweis-Ergänzungen und weitere Kurven, für die im Buch kein Platz mehr war. Wenn Sie hier etwas nicht verstehen, lesen Sie im Buch. Falls Sie Fehler finden ober noch Fragen übrig sind, wenden Sie sich an mich.

4.1 Versiera

4.2 Kubiken

4.3 Cassini u.a.bipolare Kurven

4.4.1 und 4.4.2 Lemniskate

BMG- Lemniskate Zusatz

4.4.3-4.4.7 Gelenke

Kap: Seite 4.3: S. 99	In Aufgabe 4.4. Top 2 Descartes'sche Ovale gibt es viel dazu. Siehe auch	Abb. 4.16 Bei bipolaren Kurven müssen die Abstände eines Punktes von zwei festen Punkten eine vorgegebene Gleichung erfüllen. (Genaue Definition s.u.)
	Bei den Descartes'schen Ovalen ist es eine lineare Gleichung. Für das Bild ist m = 3, n = 1, k = 1 gewählt. a) P erfüllt mit r = 5/4 und r'=11/4 die Gleichlung. b) Die rote Kurve besteht aus genau den Punkten, deren Abstände die rot geschriebene Gleichung erfüllen. Sie ist das durch diese Gleichung beschriebene Descartes'sche Oval. Ausfühliche Untersuchung der Descartes'schen Ovale siehe unten.
Kap: Seite 4.3.4: S. 101		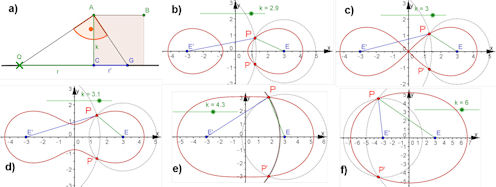Abb. 4.17 Cassini’sche Kurven: a) Geometrische Realisierung der Definitionsgleichung mit dem Höhensatz, b) bis f) Kurven für verschiedene k, c) ist speziell die Bernoulli’sche Lemniskate im GeoGebra-Book    download
	Definition 4.4 (Cassini'sche Kurven) Eine Cassini'sche Kurve ist die Ortslinie aller Punkte P, die von zwei festen Punkten E und E' ein konstantes Abstandsprodukt haben. Es gilt also für die Abstände r und r' von E bzw. E': r mal r' = k^2 mit einer reellen Zahl k.
Kap: Seite 4.3.2.3: S. 106		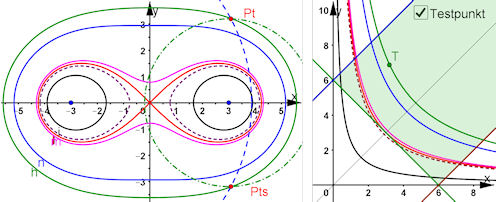Alle Cassini'schen Kurven gekoppelt mit ihren Hyperbeln und einem Testpunkt für die interaktive Erkundung download
	Definition 4.3 Bipolare Kurven allgemein Gegeben seien zwei Pole, oft auch Brennpunkte genannt, E und E' im Abstand EE' = 2e. Jeder Punkt der Ebene hat von E einen Abstand r und von E' einen Abstand r'. Jede Gleichung mit r und r' definiert eine bipolare Kurve als Menge aller Punkte, die die Gleichung erfüllen. Beispiele: Ellipsen, Hyperbeln, Descartes'sche Ovale, Cassini'sche Kurven, Bernoulli'sche Lemniskaten
Kap: Seite 4.3:S. 99ff Zusatz		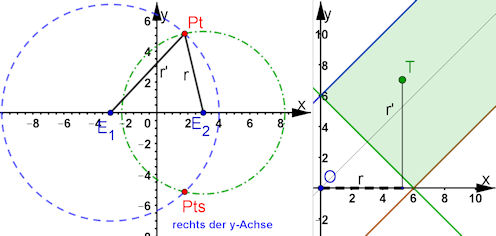Ein frei beweglicher Punkt T=(r, r') im zweiten Grafikfenster liefert die Kreisradien für das 1. Grafikfenster. Msn kann so erkunden, wann sich die Kreise schneiden, wann sich also rote Schnittpunkte ergeben. Grün ist der Gültigkeitsbereich. Liegt T auf einer der drei Grenzgeraden, berühren sich die Kreise, Pt und Pts fallen zusammen: rechts von E für T auf blauer Geraden, links von E' für T auf brauner Geraden, zwischen E und E' für T auf grüner Geraden.
	im GeoGebra-Book    download Vortrag: Kurven mit Tiefe, Schwerpunkt: Bipolare KurvenSept. 2017 in Saarbrücken.	Mathematica-Notebook Das Mathematica-Notebook zum Lesen
Kap: Seite 4.3: S. 100 Zusatz		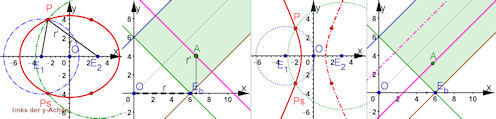Ellipsen und Hyperbeln als bipolare Kurven Geraden parallel zu y=x ( also r'=r) im Gültigkeitsbereich erzeugen Hyperbeln. Geraden senkrecht dazu erzeugen ihren Strecken im Gültigkeitsbereich Ellpsen. download
Kap: Seite 4.3.2: S. 104		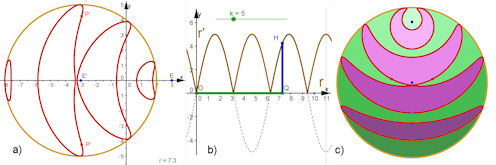Abb. 4.18 a) Bipolare Kurve mit Sinus-Gleichung, b) mit r = x (grüne Strecke) und r'= y (blaue Strecke) ist die Gleichung r' � = |k sin(r)| gezeigt, c) wie a), aber mit k=7 und um 90° gedreht (siehe auch Abb. 4.19). im GeoGebra-Book    download
Kap: Seite 4.3.2: S. 105	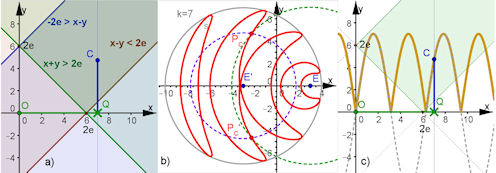im GeoGebra-Book    download	Mit Gültigkeitsbereich, siehe oben Abb. 4.19 a) Bereich fur bipolare Kurven im 2. Grafikfenster, b) bipolare Kurve im 1. Grafikfenster. Sie ist auch in Abb. 4.18 c) gefärbt und gedreht zu sehen, c) zugehörige Gleichung r' = |k sin(r)| für k=7 im 2. Grafikfenster mit gültigem Bereich.
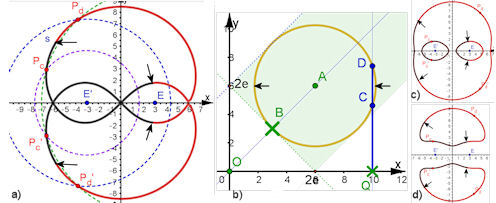
Kap: Seite 4.3.2.1: S. 106		Abb. 4.20 a) Bipolare Kurve aus Kreisgleichung im 1. Grafikfenster, b) Gültigkeitsbereich mit dem definierenden Kreis im 2. Grafikfenster, c) bipolare Kurve, wenn der definierende Kreis über den Gültigkeitsbereich hinaus ragt, d) wenn er ganz im Gültigkeitsbereich liegt. im GeoGebra-Book    download
	Wie im Buch erwähnt, ist es spannend, sich klar zu machen, welche Kurventeile von C und welche von D erzeugt werden. Dieses Bild ist noch deutlicher gestaltet: C erzeugt den roten Teil und D den schwarzen. Die Nahtstellen sind durch die Pfeile gekennzeichnet.
Kap: Seite 4.3.2.3: S. 106		Alle Cassini'schen Kurven gekoppelt mit ihren Hyperbeln und einem Testpunkt für die interaktive Erkundung download
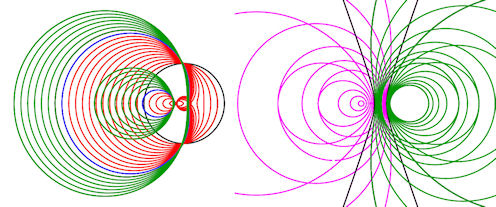
Kap: Seite 4.3.2: S. 107 Zusatz- Erkenntnisse	pur, eine Gerade, download Descartes'sche Ovale, gekoppelt mit ihren vier Geradeng0-g1g0-g2g1-g2	Aufgabe 4.4 Weitere bipolare Kurven Top 2. Descartes'sche Ovale Definition steht auch oben Lineare Gleichung m r + n r' = k In der Aufgabenlösung ist eine implizite Gleichung hergeleitet, bei der nur Quadrate der Parameter vorkommen. Wenn man sie zeichnet, entstehen i.d.R zwei Kurven. Diese entsprechen den beiden Geraden (von vier durch Vorzeichenwahl von m, n, k möglichen), die den Gültigkeitsbereich treffen.
	Gezeichnet mit der impliziten Gleichung:    e variiert, download     m variiert, download
Kap: Seite 4.3: S.107		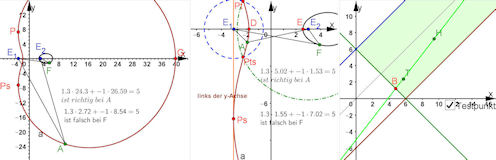Aufgabe 4.4 Weitere bipolare Kurven Top 2. Descartes'sche Ovale, Fortsetzung Weitere Überlegungen und Berechnungen sind in der Aufgabenlösung aufgegriffen. Suche nach der Beule, download
Kap: Seite 4.3.2: S. 107		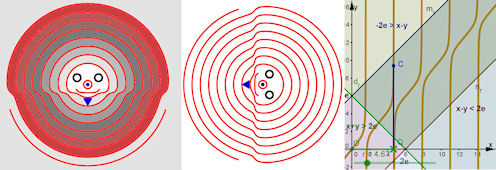Aufgabe 4.4 Weitere bipolare Kurven Top 3.: Schräger Tangens, Grinsekatze, Tangens download, Ähnliche Überlegungen beim Sinus-Teddy
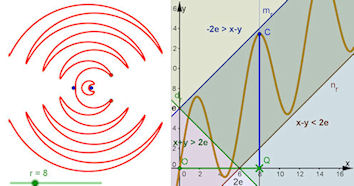
Kap: Seite 4.3.2: S. 107 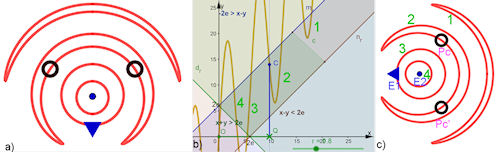Zusatz- Erkenntnisse		Aufgabe 4.4 Weitere bipolare Kurven Top 4.: Schräger Sinus 4. Sinus download Top 4.: Schräger Sinus-Teddy Die grünen Zahlen in der Mitte entsprechen den grünen Zahlen im rechten Bild. der Teddy entsteht vollständig in GeoGebra, es ist kein Malprogramm beteiligt. Das gilt auch für die Parabelköpfe und die Grinsekatze. In letzterer sind lediglich die Farbfüllungen ein Malprogramm-Effekt. download
Kap: Seite 4.3.2: S. 107 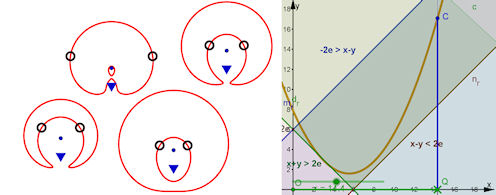Zusatz- Erkenntnisse	download	Aufgabe 4.4 Weitere bipolare Kurven Top 5. Parabelrelation als bipolare Kurve Welcher Kopf gehört zu der rechts im Gültigkeitsbeeich gezeigten Parabel? Was passiert, wenn man eine Parabel wählt, die rechte untentere Kante des Gültigkeitsbereiches auch noch schneidet? Was ist, wenn man die Parabel dreht, z.B. mit dem Drehungswerkzeug von GeoGebra? Kann man es schaffen, dass die Köpfe in Unendliche reichen, wie z.B. die Hyperbeln? Man kann hier auch einiges genau ausrechnen! Stellen Sie sich selbst noch drei Fragen!

Prof. Dr. Dörte Haftendorn	Erstellt August 2016, Update 09.01.2018	www.kurven-erkunden-und-verstehen.de