04 Barocke Blüten und Früchte   Logo der Berliner Mathematischen Gesellschaft Logo der Berliner Mathematischen Gesellschaft
|
| Anlass und Erläuterung zu dieser Seite. |  Die Berliner Mathematische Gesellschaft, BMG, hat mich zu einem Vortrag: "Kurven verstehen durch zwei Perspektiven" eingeladen, der am 8.2.2018 in Berlin stattfand. Er ist auf dieser Site hier verlinkt. Drei Konstruktionen des Logos der BMG habe ich dort vorgestellt, im Folgenden zeige ich diese und noch weitere Erzeugungen. Sie sehen jeweils ein Bild des Ergebnisses, die Eräuterungen und Beweise und die zugehörige GeoGebra-Datei. Die Berliner Mathematische Gesellschaft, BMG, hat mich zu einem Vortrag: "Kurven verstehen durch zwei Perspektiven" eingeladen, der am 8.2.2018 in Berlin stattfand. Er ist auf dieser Site hier verlinkt. Drei Konstruktionen des Logos der BMG habe ich dort vorgestellt, im Folgenden zeige ich diese und noch weitere Erzeugungen. Sie sehen jeweils ein Bild des Ergebnisses, die Eräuterungen und Beweise und die zugehörige GeoGebra-Datei. | ||
BMG-Lemniskate als Mittenkurve |
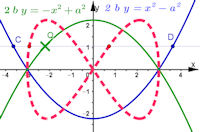
Es ist a=3 und b=2. Q wandert auf der grünen Parabel. Die Gerade y=y(Q) schneidet die blaue Parabel in C und D. Die Ortskurve von P, der Mitte der Strecken CQ bzw. QD, ist eine (allg.) Gerono'sche Lemniskate. Speziell für a=3 und b=2 ist die die BMG-Lemniskate 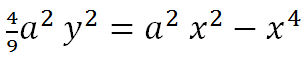 gezeigt. gezeigt.
| BMG-Lemniskate als Mittenkurve Die Geronosche Lemniskate ist in meinem Kurven-Buch in Kapitel 4.4.3.1 auf Seite 117 als Mittenkurve zu zwei Parabeln dargestellt, die im Vergleich zu den Parabeln links nur einen Parameter a=b haben. Für die Anpassung an das BMG-Logo ist ein zweiter Parameter b nötig. Die so erhaltenen Kurven werden nun Gerono'sche Lemniskaten genannt. Deren explizite algebraische Gleichung ist Das BMG-Logo ist eine spezielle Gerono'sche Lemniskate, und zwar ist b=2/3 a nötig. Sie sei im Folgenden als BMG-Lemniskate bezeichnet. | |
| Für die echte Gerono'sche Lemniskate sind im Buch Beweise und drei weitere Konstruktionen in Aufgabe 4.8. Zwei davon lassen sich anpassen: BMG-Lemniskate als allgemeine Versiera und BMG-Lemniskate aus Gerade und Ellipse. Es folgen zunächst die beiden Darstellungen aus dem Vortrag. Sie sind als (allg.) Gerono'sche Lemniskaten beschrieben. | |||
BMG-Lemniskate als Lissajous-Kurve |
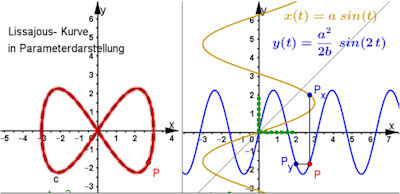 BMG-Lemniskate als Lissajouskurve BMG-Lemniskate als Lissajouskurve in zwei Perspektiven Rechts ist der Graph der Parametergleichung für y blau dargestellt. Zu einem Wert von t, grün gestrichelt, auf der Rechtsachse gehört der Punkt Py. Der Graph der Parametergleichung für x ist zunächst auch als Funktion dargestellt worden, dann aber an der Geraden y=x gespiegelt und in Ocker zu sehen. Zu einem t gehört Px. Dann gilt P=(x(Px), y(P(y)). Dieser rote Punkt ist dann auch in dem linken Fenster dargestellt und bildet dort bei Variation von t die BMG-Lemniskate. | ||
Beweis der Parametergleichungen: Aus der oben genannten expliziten Gleichung folgt bei Ersetzung von x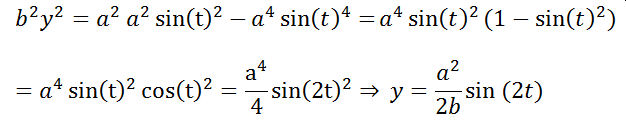
| |||
BMG-Lemniskate als Polarkurve |
 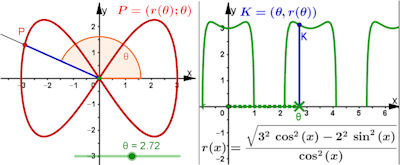 BMG-Lemniskate als Polarkurve BMG-Lemniskate als Polarkurve in zwei Perspektiven Beweis der Polargleichung: 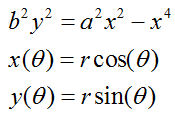 Einsetzen und Auflösung nach r ergibt 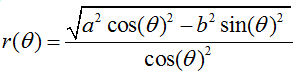  Die Werte des Polarwinkels, die den Radikanden der Wurzel negativ machen, erzeugen keinen Bildpunkt in dem Sektor des Logos, in dem B steht. Die Werte des Polarwinkels, die den Radikanden der Wurzel negativ machen, erzeugen keinen Bildpunkt in dem Sektor des Logos, in dem B steht.
| ||
BMG-Lemniskate als allg. Versiera |
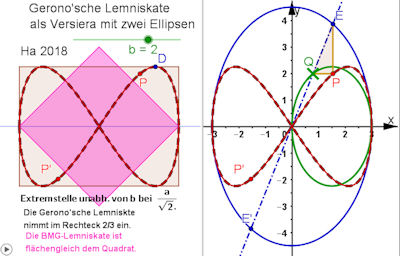 BMG-Lemniskate als Versiera BMG-Lemniskate als VersieraIm Buch ist die Versiera der Maria Agnesi ausführlich behandelt. Es gibt eine Verallgemeinerung von Lockwood(1962), die hier verwendet wird: Bei einer allgemeinen Versiera wandet Q auf einer Kurve C1, die Gerade OQ schneidet eine zweite Kurve C2 in E (und E'). P erbt die Abszisse von E und die Ordinate von Q. | ||
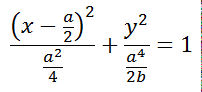 Bei der echten Gerono'schen Lemniskate sind die Kurven C1 und C2 Kreise. Es ist klar, dass C1 durch den rechten Scheitel der BMG-Lemniskate und durch O verlaufen muss. Wenn man C1 als Ellipse ansetzt, muss sie die gezeigte Gleichung haben, denn die senkrechte Halbachse ist die Scheitelordinate der Parabel für die Mittenkurve. Bei der echten Gerono'schen Lemniskate sind die Kurven C1 und C2 Kreise. Es ist klar, dass C1 durch den rechten Scheitel der BMG-Lemniskate und durch O verlaufen muss. Wenn man C1 als Ellipse ansetzt, muss sie die gezeigte Gleichung haben, denn die senkrechte Halbachse ist die Scheitelordinate der Parabel für die Mittenkurve.
Für die blaue Ellipse Die Idee ist, dass Q in im oberen Scheitel der grünen Ellipse das Maximum der Lemniskate erzeugt. Dessen Abszisse ist also die Abszisse von E. Mit dem Strahlensatz hat man die Ordinate von E und damit einen Punkt auf der blauen Ellipse. Damit ergibt sich: Der Beweis, dass sich durch diese Konstruktion wirklich die (allg.) Gerono'sche Lemniskate ergibt, erfolgt wie im Buch nach Satz 4.1 auf Seite 88 und ist in der Mathematica-Datei durchgeführt. Alle Gerono'schen Lemniskaten nehmen 2/3 des umbeschriebenen Rechtecks ein. Die Integration ist in der Mathematica-Datei durchgeführt. Speziell die BMG-Lemniskate hat den Flächeninhalt 2 a^2. Er ist visualisiert in dem violetten Quadrat im obigen Bild. Die Maximumstelle aller Gerono'schen Lemniskaten hängt nur von a ab, nicht von b. Sie ist a/Wurzel(2). Sie lässt sich aber auch konstruieren (wenn man dies weiß), indem man das violette Quadrat mit y=x und y=-x viertelt und die Kantenlänge eines solchen Viertelquadrates von O aus auf der x-Ache abträgt. | |||
BMG-Lemniskate aus Gerade und Ellipse |
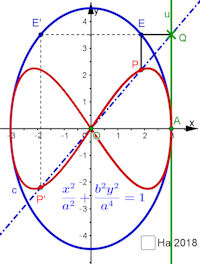
| BMG-Lemniskate aus Gerade und Ellipse Auch mit dieser verblüffend einfachen Konstruktion entstehen alle Gerono'schen Lemniskaten. Die Ellipse ist mit dem Faktor a/b aus dem Kreis mit dem Radius a gesteckt. Schreibt man die Ellipsengleichung mit v anstelle von y und verwendet den Strahlensatz für Q=(a,v) und P=(x,y) als vx=ay, folgt aus der links angegebenen Ellipsengleichung sofort 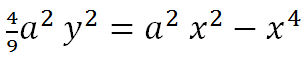 . .
| |
| www.kurven-erkunden-und-verstehen.de | ||