Kurven erkunden und verstehen, Website zum Buch

04 Barocke Blüten und Früchte

4.4.3 bis 4.4.7 Gelenke, Stangen, Sonder-Zirkel und Technik

Website zum Buch: Hier sind die Dateien, die die Bilder des Buches erzeugt haben, die Aufgabenlösungen, Beweis-Ergänzungen und weitere Kurven, für die im Buch kein Platz mehr war. Wenn Sie hier etwas nicht verstehen, lesen Sie im Buch. Falls Sie Fehler finden ober noch Fragen übrig sind, wenden Sie sich an mich.

4.1 Versiera

4.2 Kubiken

4.3 Cassini u.a.bipolare Kurven

4.4.1 und 4.4.2 Lemniskate

BMG-
Lemniskate

Zusatz

4.4.3-4.4.7 Gelenke

Kap: Seite 4.4.3.1: S. 119		Abb. 4.30 Gelenke für höhere Kurven: a) Bernoulli’sche Lemniskate, b) Konchoide des Nikomedes, c) Strophoide und Cissoide (Quelle: http://www.macchinematematiche.org/) Surfen Sie in der Sammlung der Universität Modena in Italien! Man kann solche Gelenke auch mit Pappen und Briefklammern nachbauen.

Kap: Seite 4.4.4.1: S. 121		Abb. 4.31 Frans van Schooten (jr.) 1615-1660, „Mathematische oeffeningen“, Bibliothek Utrecht, 544 Seiten, enthält ein großes Kapitel über Kegelschnitte Quellen, auch für die nachfolgenden Bilder von Frans van Schooten: Bibliothek der Universität Utrecht, Volltext: http://hdl.handle.net/1874/20606, Portrait von 1656 (P.Koninck) home.planet.nl/~hietb071/fvs_frans.htm

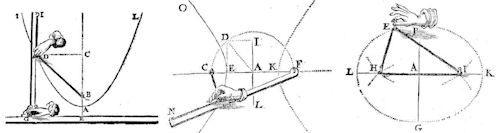
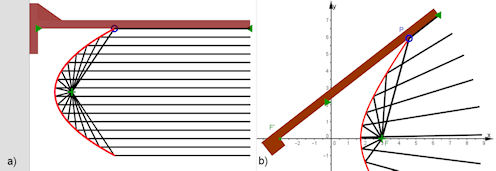
Kap: Seite 4.4.4.1: S. 122		Abb. 4.32 Echte Fadenkonstruktionen der Kegelschnitte: a) Parabel, b) Hyperbel, c) Ellipse (Frans van Schooten, in obigem Volltext von 1659, S.299ff) Abb. 4.33 Realisierungen in Holz: a) Parabellineal mit Faden b) Hyperbellineal mit Faden Aus Holzstangen, etwa einen Meter lang, kann dieses zum Einsatz an der Schultafel nutzen. Dazu passt die "Gärtner-Konstruktion der Ellipse",Abb.4.32 c), bei der man nur einen Faden braucht (Länge 2a=langer Duchmesser) im GeoGebra-Book Parabellineal, download im GeoGebra-Book Hyperbellineal, download

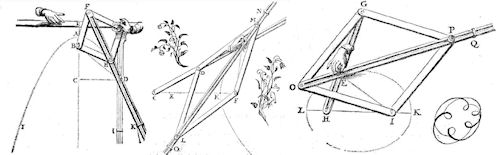
Kap: Seite 4.4.4.2: S. 123		Abb. 4.34 Rautengelenke für die Kegelschnitte: Parabel, Hyperbel und Ellipse (Frans van Schooten) Sie noch einmal auf Abb. 4.33 und denken Sie sich eine Mittelsenkrechte zu der Strecke, die der Brennpunkt und der linke grüne Punkt miteinander bilden. Diese Mittelsenkrechte können sie in Abb. 4.10 auch sehen. Dann erkennen Sie, dass genau diese Mittelsenkrechte von den Rautenkonstruktionen in Abb. 4.34 als lange Stange mit Führungsrille zu sehen ist.
	Der Zeichenstift muss weiterhin so geführt werden wie bei der Fadenkonstruktion, die bewegliche Raute gibt Stabilität und dient zur Vermeidung des "wackeligen" Fadens. Wie oben schon gesagt, kann man solche Gelenke auch mit Pappen und Briefklammern nachbauen. Eine Realisation in GeoGebra ist auch möglich, im Folgenden sind solche Gelenkkonstruktionen verwiklicht.
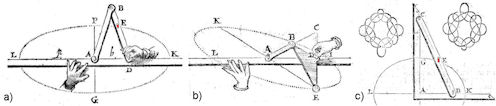
Kap: Seite 4.4.5.1: S. 125		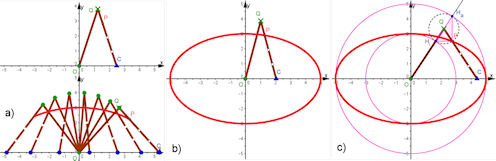Abb. 4.35 Ellipsen a) Ellipsen-Zirkel für die gerade Ellipse, b) Zirkel für schräge Ellipsen, b) Stangenkonstruktion der Ellipse (Frans van Schooten) Abb. 4.36 Realisierungen in GeoGebra a) Der Ellipsenzirkel aus zwei gleichlangen Stangen, b) Der Stift in einem der Löcher zeichnet eine Ellipse, c) Beweis durch Bezug zur Ellipsenkonstruktion als allgemeine Versiera mit Haupt- und Nebenscheitelkreis, Abb. 4.9 im GeoGebra-Book download

Kap: Seite 4.4.5.2: S. 125		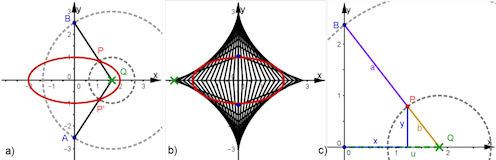Abb. 4.37 Stangenkonstruktion der Ellipse oder „rutschende Leiter“ a) Gesamtbild b) Astroide als Hüllkurve der Stangen c) Beweisfigur im GeoGebra-Book download
	Achtung: die gezeigte Konstruktion erzeugt wegen des zweiten Schnittpunktes mit dem kleineren grauen Kreis unten rechts noch einen weiten Punkt. Der sorgt bei Anforderung der Ortslinie für ein zweite Ellipse. In der ggb-Datei ist das durch Verwendung des Strahlenssatzes vermieden. Zudem kann man in der Datei den geschickten Gebrauch von "Anzeigebedingungen" lernen.
Kap: Seite 4.4.6.1: S. 126		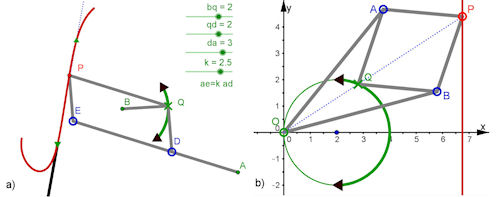Abb. 4.38 Gelenke, die in Machinen eine Kreisbewegung in eine gerade Bewegung umwandeln a) Geradführung an der Dampfmaschine von James Watt, Watt-Parallelogramm, b) Inversor von Peaucellier, siehe Abschnitt 4.4.6.3 im GeoGebra-Book Watt-Lemniskate, download im GeoGebra-Book Inversor von Peaucellier, download

Kap: Seite 4.4.6.1: S. 127		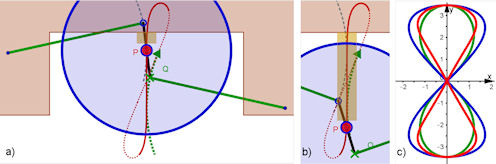Abb. 4.39 a) und b) Watt-Mechanismus oder Lemniskaten-Anlenkung: Die Stöße auf das Rad werden nicht auf den Wagen übertragen. In Bild c) sind – mit gleichen Halbachsen – in Rot die Watt’sche, in Grün die Bernoulli’sche und in Blau die Gerono’sche Lemniskate zu sehen. im GeoGebra-Book Watt-Anlenkung, download im GeoGebra-Book Drei Lemniskaten,download

Kap: Seite 4.4.6.2: S. 127		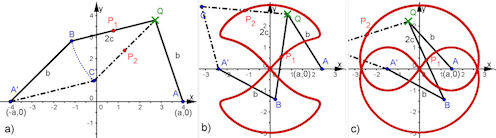Abb. 4.40 Watt’sche Kurven: A = (a, 0), a) Gelenkkonstruktion für die rote Kurve in Abb. 4.39 c): a=b=4, c=2, Bild b) Gelenk mit a=2.4, b=3, c=2, Bild c) Gelenk mit a=1.5, b=3, c=2 im GeoGebra-Book download

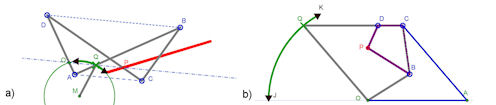
Kap: Seite 4.4.6.4: S. 129 Aufgabe 4.9		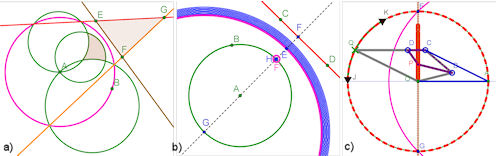Abb. 4.41 a) Inversor von Hart b) Drachen-Gelenk von Kempe, im GeoGebra-Book download im GeoGebra-Book Drachen-Gelenk pur, download Aufgabe 4.9 Mit der Inversion spielen, Drachen von Kempe a) Afg4.9 zu 1. b) Afg4.9 zu 3. c) Kempe im GeoGebra-Book Afg4.9 zu 4.

Kap: Seite 4.4.6.5: S. 131		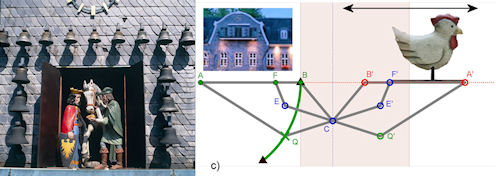Abb. 4.42 Der Doppeldrachen von Kempe kann Figuren schieben: Beim Glockenspiel an der ehemaligen Kämmerei in Goslar kommt in der Mitte der Ritter Ramm mit seinem Pferd heraus, hier kommt das Huhn. Für das schöne Foto links danke ich der GOSLAR marketing gmbh. im GeoGebra-Book download
	In Abb. 4.42 sind wie schon in Abb. 4.41 b) große und kleine Drachen (Rhomboide), die untereinander mathematisch ähnlich sind, zu sehen. Das Gestänge ist in jeder Stellung zu der gestrichelten Geraden durch C symmetrisch. Wandert Q auf dem Kreisbogen nach oben, so werden die Drachen schmaler, C rückt nach rechts und das Huhn kommt ganz aus dem durch die getönte Fläche angedeuteten „Kasten“ hervor. Umgekehrt verschwindet das Huhn ganz im Kasten, wenn Q den tiefsten Punkt des Bogens erreicht. Am ehemaligen Kämmereigebäude am Marktplatz von Goslar ist im Giebel ein Glockenspiel mit Figurenumlauf angebracht. Gegen Ende der Musik geht in der Mitte eine Tür auf und der Ritter Ramm mit seinem Pferd und Kaiser Otto I. werden herausgeschoben. Der Sage nach hat das Pferd am Berg im Boden gescharrt, so dass Silber zum Vorschein kam. Seither hat über tausend Jahre lang das Silber aus dem „Rammelsberg“ der Stadt Goslar Reichtum gebracht. Leider ist die „Silberquelle“ versiegt, aber das Weltkulturerbe bringt nun die Touristen nach Goslar. In Kirchen stehen manches Mal Haus- oder Kirchenmodelle, bei denen sich nach dem Einwurf einer Münze eine Tür öffnet und eine segnende Engelsfigur hervorgeschoben wird. Ich habe es in Falkenberg in der Oberpfalz und in Kloster Schönau an der Fränkischen Saale gesehen. Es entzieht sich meiner Kenntnis, welcher Mechanismus die Figuren bewegt, aber es könnte etwa dieser von Kempe sein.