04 Barocke Blüten und Früchte 4.1 Versiera, die Hexenkurve

Website zum Buch: Hier sind die Dateien, die die Bilder des Buches erzeugt haben, die Aufgabenlösungen, Beweis-Ergänzungen und weitere Kurven, für die im Buch kein Platz mehr war. Wenn Sie hier etwas nicht verstehen, lesen Sie im Buch. Falls Sie Fehler finden ober noch Fragen übrig sind, wenden Sie sich an mich.

4.1 Versiera

4.2 Kubiken

4.3 Cassini u.a.bipolare Kurven

4.4.1 und 4.4.2 Lemniskate

BMG- Lemniskate Zusatz

4.4.3-4.4.7 Gelenke

	Versiera, die Hexenkurve Zitiert aus dem Buch: Bevor ich Ihnen wieder eine allgemeine Definition gebe, möchte ich die erste Mathematik-Professorin Italiens --~vermutlich sogar Europas~-- vorstellen: Maria Gaetana Agnesi aus Mailand (sprich Anjesi). Die 1718 geborene Tochter eines vermögenden Seidenfabrikanten fiel schon als Kind durch ihre Begabung auf und der Vater verschaffte ihr die besten Privatlehrer für Mathematik. Mit dreißig Jahren veröffentlichte sie 1748 ein Buch mit dem Titel "`Einführung in die Analysis für den Gebrauch der italienischen Jugend"'. Es enthält nicht so sehr eigene mathematische Ergebnisse als vielmehr sorgfältig ausgewählte Beispiele, die mathematische Ideen veranschaulichen. Dieses Buch und der ein Jahr später folgende zweite Teil fanden viel Beachtung und Anerkennung, z.B. auch bei der französischen Akademie der Wissenschaften. Dieses zitiere ich nach O'Connor und Robinson {mactutor1999}. Die Autoren erzählen auch, dass der Name "Hexenkurve" auf einem Übersetzungsfehler beruht. Schon zu Anfang des 18. Jahrhunderts hatte Fermat die Kurve vorgestellt und sie lateinisch "`versoria"' genannt, Grandi italienisierte dieses zu "`versiera"'. Man weiß nicht, ob es von sich hinwenden (die Kurve wendet sich zur x-Achse hin -- was ich vermute~--) kommt, oder von einem Seil, mit dem man Segel in eine andere Richtung wendet. Maria Agnesi hat die Bezeichnung Versiera verwendet. Jedenfalls ist vom Übersetzer ihres Werkes ins Englische das Wort "`l'avversiera"' gelesen worden, das eine "`witch"', eine "`Hexe"', bezeichnet. Dadurch wird im englischen Sprachraum gesprochen von "`the Witch of Agnesi"', das wort curve wird fortgelassen. Dieser Sprachregelung folgen --~nach Wikipedia in diversen Sprachen~-- die Franzosen mit sorcière, die Spanier mit bruja und die Schweden mit \textit{häxa}. Lediglich die Italiener selbst sagen einfach \textit{versiera}, erläutern dann allerdings den Übersetzungsfehler, der zu \textit{witch} geführt hat, im heutigen Italienisch \textit{strega}. Die Hexenkurve, also die Versiera der Maria Agnesi, ergibt sich nicht durch Hexerei sondern auf einfache Weise geometrisch.
Kap: Seite 4.1: S. 80		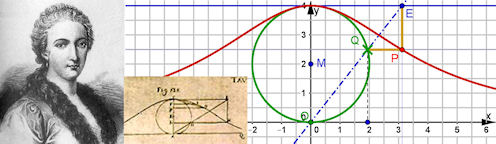Abb. 4.1 Abb. 4.1 Maria Agnesi (1718-1799) und die Konstruktion der Versiera (Quelle für das Portait: Wikipedia Commons, gemeinfrei, für die alte Zeichnung, [Agnesi 1748]) im GeoGebra-Book    download
Kap: Seite 4.1.1.2: S. 81		Abb. 4.2Vollständige Berechnung der Krümmung mit GeoGebra-CAS im GeoGebra-Book    download
Kap: Seite 4.1.2.1: S. 83	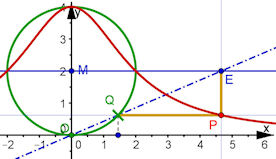Konstruktion Auf einem Kreis um M = (0, a) mit dem Radius a wandert zugfest Q. Die Parallele zur x-Achse durch M schneidet Gerade OQ in E. Der Punkt P = (x, y) hat die Abszisse von E und die Ordinate von Q. P ist demnach die rechtwinklige Ecke eines Steigungsdreiecks QPE für die Gerade g. Die Ortslinie von P bezüglich Q ist die enge Versiera.	Abb. 4.3 Enge Versiera im GeoGebra-Book    download
Kap: Seite 4.1.3: S. 84		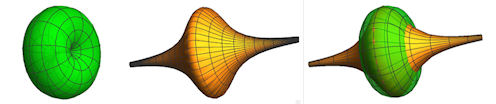Abb. 4.4 Rotation der engen Versiera und volumengleicher Torus aus dem Erzeugungskreis Diese Bilder sind mit Mathematica gemacht, inzwischen geht es auch in GeoGebra mit dem Befehl Oberfläche[....].
	Es ist eine lohnende Aufgabe, die enge und auch die weite Versiera um die x-Achse rotieren zu lassen. Mit den Integralen hat man keine schwierigkeiten, da man nach y^2 auflösen kann. Es kommen uneigentliche Integrale vor und sie bilden "schöne" Verhältnisse untereinander. Die Tori können mit der Formel V(Torus)=2 pi^2 R^2 d leicht berechnet werden. Der Torus Querschnitt ha Radius R. Sein Mittelpunkt Abstand d von der Drehachse.
Kap: Seite 4.1.3.2: S. 85		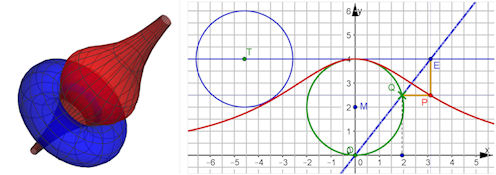Abb. 4.5 Rotation der weiten Versiera (Im Buch ist die rechte Bildhälfte nicht hier sondern im nächsten Absatz.) Wegen der Achsenstreckung ist das Volumen doppelt so groß wie bei der engen Versiera. Bei gleichem Drehkreisradius ist nun ein Loch in dem volumengleichen Torus.
	Der Mittelpunkt des Drehkreises hat die doppelte Entfernung von der Drehachse. V = 4pi^2a^3 = 2pi^2a^2 mal 2a. Die Stellung des Drehkreises im Querschnitt, die im Wimmelbild Abb. 4.6 gezeigt ist, wurde in GeoGebra "nach Sicht"� gefunden.
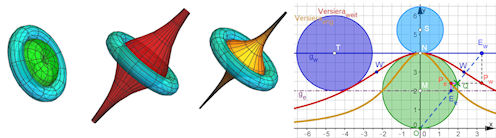
Kap: Seite 4.1.3.2: S. 85		Abb. 4.6 Beide Versierae und ihre Tori, Wimmelbild zu Aufgabe 4.2 Die Rotationskörper entstammen wieder Mathematica. Das Wimmelbild aber ist aus GeoGebra.
	im GeoGebra-Book    Wimmelbild download   Gemeinsamer Schwimmgürtel-Torus
Kap: Seite 4.1.4.1: S. 87	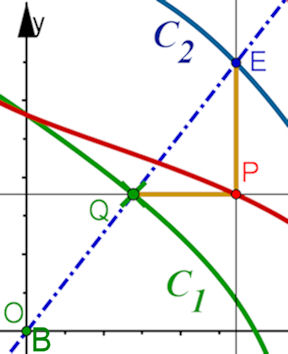Diese Verallgemeinerung habe ich weder in Büchern noch im Internet gefunden. Sie ist aber sehr naheliegend. Sinnvoll ist sie, da sie Erkundungen ermöglicht, aber auch die Scheitelkreiskonstruktion der Ellipse liefert. Ein Frage ist, ob das Vertauschen von C1 und C2 dieselbe Kurve liefert!?!?!?!	Abb. 4.7 Allgemeine Versiera mit ihrer geometrischen Konstruktion aus zwei Kurven. Charakterisch für die Versiera-Konstruktion ist das kleine Steigungsdreieck mit der Hypotenuse Strecke QE und seiner rechtwinkligen Ecke als definierendem Punkt P, wie es in Abb. 4.1 und Abb. 4.3 und hier allgemein zu sehen ist. download
Kap: Seite 4.1.4.2: S. 88		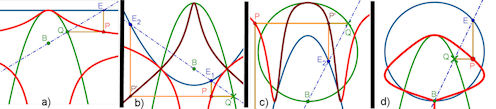Abb. 4.8 Beispiele zur allgemeinen Versiera: a)Parabel–Gerade, b) Parabel–Parabel, c) Kreis– Parabel, d) Tausch von C1 und C2 bei c), also Parabel–Kreis.
	Wenn C2 eine explizite Funktionsgleichung hat, sind in Satz 4.1 im Buch die Versieragleichungen schon allgemein hergeleitet. Auch wenn das nicht der Fall ist, sind die beiden Gleichungen, aus denen man nur noch zwei Parameter eliminieren muss, schon angegeben (und bewiesen). Also lohnt sich die Behandlung der Versiera auf vielfältige geometrische und analytische Weise. Drei umfassende Ekundungsaufgaben stehen im Buch. im GeoGebra-Book        Parabel-Parabel: download    Kreis-Parabel: download    Kreis-kreis: downloadKreis-kreis ganz frei:download      allg. Funktionen: download    Ellipse-hyperbel: download
Kap: Seite 4.1.4.4: S. 90		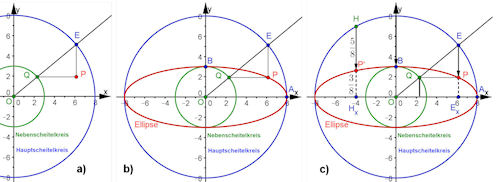Abb. 4.9 Ellipse in Scheitelkreiskonstruktion als (allgemeine) Versiera: a) Konstruktion, b)Ellipse als Versiera, c) Ellipse als gestauchter Kreis. Es ist phi = winkel(AOE). im GeoGebra-Book    download
	Aus diesem Zusammenhang wird im Buch auf vier!!! verschiedene Arten die Mittelpunktsgleichung der Ellipse und ihre übliche Parameterdarstellung hergeleitet.

Inhalt und Web:  Prof. Dr. Dörte Haftendorn	Erstellt August 2016, Update 01.09.2024	www.kurven-erkunden-und-verstehen.de