|
04 Barocke Blüten und Früchte 
4.4.1 & 4.4.2 Lemniskate |
| Website zum Buch: Hier sind die Dateien, die die Bilder des Buches erzeugt haben, die Aufgabenlösungen, Beweis-Ergänzungen und weitere Kurven, für die im Buch kein Platz mehr war. Wenn Sie hier etwas nicht verstehen, lesen Sie im Buch. Falls Sie Fehler finden ober noch Fragen übrig sind, wenden Sie sich an mich. |
4.1 Versiera  | 4.2 Kubiken |
4.3 Cassini u.a.bipolare Kurven | 4.4.1 und 4.4.2 Lemniskate  |  BMG-Lemniskate Zusatz |
4.4.3-4.4.7 Gelenke |
| Kap: Seite 4.4.1: S. 108 |
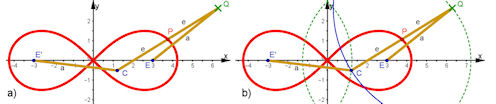 | Abb. 4.21 Bernoulli’sche Lemniskate aus einer Gelenk-Konstruktion, siehe Abschnitt 4.4.3.1
 im GeoGebra-Book
download
| ||
| Kap: Seite 4.4.1: S. 109 |
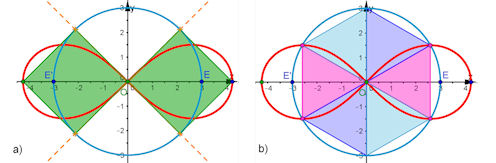 | Abb. 4.22 Lemniskate: a) Tangenten im Ursprung und Flächeninhalt der Lemniskate, er ist
gleich dem der beiden Quadrate mit Kantenlänge e, b) Extrema in den Sechseckspunkten
im GeoGebra-Book
Flächen=Quadrate, download
im GeoGebra-Book
Extrema auf Sechseck, download
| ||
| Kap: Seite 4.4.1.3: S. 111 |
 im GeoGebra-Book zu Bild a), download
im GeoGebra-Book
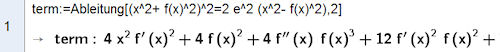
mit GeoGebra CAS, download | Abb. 4.23 Lemniskate:
a) Krümmungskreise in den Extrema, b) Krümmungskreise in den Scheiteln (hierzu Datei bei Abb. 4.24) eingefügt: Berechnung mit GeoGebra CAS | ||
| Kap: Seite 4.4.1.4: S. 111 |
 | Abb. 4.24 Krümmung am Scheitel der Lemniskate:
a) experimentelle Erkundung b) exakter Krümmungskreis und Bezüge zu anderen Eigenschaften | ||
| a) im GeoGebra-Book
a) experimentell, download
b) im GeoGebra-Book
b) geometrische Eigenschaften, download
| ||||
| Kap: Seite 4.4.1.4: S. 112 -113 Afg. 4.5 |
b) im GeoGebra-Book
b) download b) bezeichnete Version | Abb. 4.25 Lemniskate: Wimmelbild zu den Eigenschaften und ihren Bezügen, siehe Aufgabe 4.5 Auch ohne die Aufgabe zu kennen, kann man viele Eigenschaften aus dem Wimmelbild herauslesen und dann versuchen, sie zu beweisen. | ||
 Aufgabe 4.5 Lemniskaten-Eigenschaften Afg4.5 Top 6. und 7.+CAS Afg4.5 Top 9. | ||||
| Kap: Seite 4.4.1.5: S. 113 |
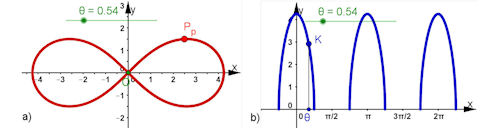 | Abb. 4.26 Lemniskate: a) Polardarstellung, mit b) der gekoppelten kartesischen Sicht Polargleichung der Lemniskate r(theta)^2=2 e^2 cos(2 theta) im GeoGebra-Book
download
| ||
| Kap: Seite 4.4.1.5: S. 114 |
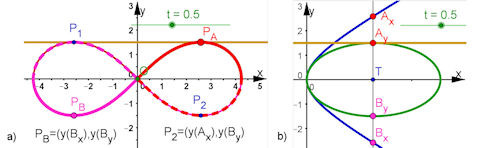 | Abb. 4.27 Lemniskate: a) erste Parameterdarstellung aus Gl. 4.28, mit b), der gekoppelten Sicht auf beide Parameterkurven x(t)^2=e^2(t+t^2) y(t)^2=e^2(t-t^2) im GeoGebra-Book
download
| ||
| Kap: Seite 4.4.1.5: S. 115 |
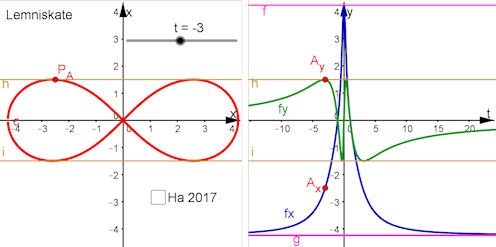 | Aufgabe 4.6 Parameterdarstellungen der Lemniskate
Top 1. download
Hiezu gehört die Abbildung. Rechts sind im 2.Grafikfenster die Funktionen fx und fy zu sehen, die im linken Grafikfenster P=(fx(t), fy(t)) erzeugen. Top 2. download
Top 3. download
| ||
| Kap: Seite 4.4.2: S. 116
|
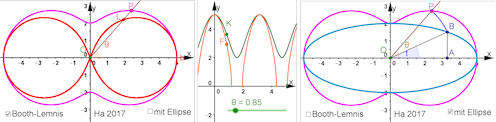 | Aufgabe 4.7 Booth'sche Ovale und Booth'sche Lemniskaten
Ausführliche Lösung mit einer zusätzlichen Betrachtung der Polargleichung. Zu 1.-5. download
Zu 6.-7. download
polar download
mit Ellipse download
Erfindung einer geometischen Konstruktion für Booth'sche Ovale
| ||
| Kap: Seite 4.4.2.1: S. 117 Aufgabe4.8 S.118 |
 a) Gerono’sche Lemniskate als Mittenkurve zweier Parabeln, Richtung senkrecht zur Parabelachse, b) Parabel als Mittenkurve zwischen Parabeln, Richtung parallel zur Parabelachse, c) Kettenlinie k(x) = cosh(x) als Mittenkurve zu f(x) = e^x und g(x) = e^(-x) d) Ellipse als Mittenkurve von Kreis und Durchmesser Bauen Sie die Dateien zu b), c) und d) selbst. c) ist auch in Kap.9.6.4 bei der Kettenlinie, d)ist Spezialfall von Abb.4.9.c) | Abb. 4.28 Mittenkurve zweier Kurven:
echte Gerono'sch Lemniskate download Man kann die Definition erweitern, indem man einen weiteren Parameter in die Parabelgleichung nimmt. Lesen Sie:
| ||
| Kap: Seite 4.4.2.1: S. 117 |
 
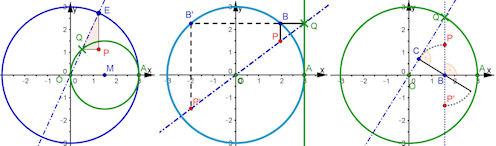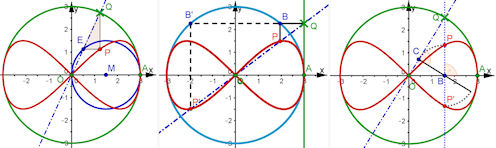
Auch die beiden ersten dieser Konstruktionen sich auf für allgemeine Gerono'sche Lemniskaten übertragbar. Lesen Sie:
| Abb. 4.29 Gerono’sche Lemniskate in drei Konstruktionen: a) Gerono’sche Lemniskate als allgemeine Versiera nach Definition 4.1, b) eine etwas andere Konstruktion, c) Konstruktion mit zwei Loten und einer Längenübertragung Aufgabe 4.8
im GeoGebra-Book
Bild a) download
im GeoGebra-Book
Bild b) download
Gerono1-2-3-Gesamtdatei
im GeoGebra-Book
Bild c) download
| ||
 Prof. Dr. Dörte Haftendorn |
 Erstellt August 2016, Update |
www.kurven-erkunden-und-verstehen.de |
| ||