Kurven erkunden und verstehen, Website zum Buch

05 Frei erfunden und hoch hinaus

5.1 und 5.2 Frei erfundene Kurven
geometrische Ideen, erfundene Gleichungen

Website zum Buch: Hier sind die Dateien, die die Bilder des Buches erzeugt haben, die Aufgabenlösungen, Beweis-Ergänzungen und weitere Kurven, für die im Buch kein Platz mehr war. Wenn Sie hier etwas nicht verstehen, lesen Sie im Buch. Falls Sie Fehler finden ober noch Fragen übrig sind, wenden Sie sich an mich.

5.1 Frei erfundene geometrisch erzeugte Kurven
Kap: Seite 01:S.1		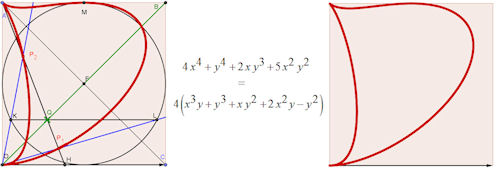Abb. 1.1 Die D-Kurve, ihre Konstruktion, ihre Gleichung und das D als pure Kurve. Näheres siehe Abschnitt 5.1.1. Konstruktion aus [Wieleitner 1919]. im GeoGebra-Book download
	5.1.1.1 Analyse einer Konstruktion Text ausführlich im Buch, Ergebnis: Konstruktion aus Quadrat, Diagonalen und Inkreis: Setze Q zugfest auf die Diagonale OB. Die Parallele zu OC schneidet den Kreis in K und L. Die Geraden OK und OL schneiden die Gerade AQ in P1 und P2. Die Ortslinien von P1 und P2 bezüglich Q bilden das D. Gleichungsherleitung für das Wieleitner-D finden Sie im Buch
Kap: Seite 5.1.1: S. 134		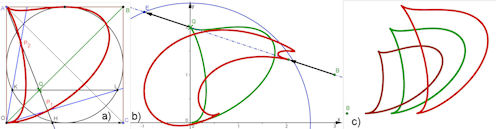Abb. 5.1 a) Konstruktion der D-Kurve von [Wieleitner 1919], b) D-Kurve und ihre Cissoide bezüglich eines Kreises c) D-Kurve und ihre Konchoide mit dem „Baum“ in B. D-Cissoide im GeoGebra-Book D-Cissoide download
	D-Konchoide im GeoGebra-Book Erläuterung zur D-Konchoide auf der Konchoiden-Seite D-Konchoide download
Kap: Seite 5.1.2: S. 135		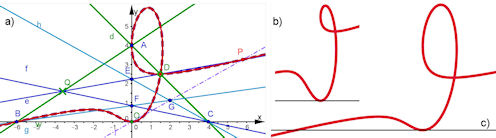Abb. 5.2 a) Konstruktion der deutsch-d-Kurve b) d-Kurve für s=0.7 c) d-Kurve für s=1.5 im GeoGebra-Book download

Kap: Seite 5.1.3: S. 136		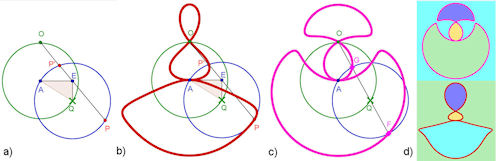Abb. 5.3 a) Konstruktion der roten Topfblumen-Kurve b) rote Topfblumen-Kurve c) violette Topfblumen-Kurve, die eine Strophoide und eine Konchoide ist d) beide Topfblumen farbig gestaltet
	Aufgabe 5.1 Topfblumen im GeoGebra-Book Sammeldatei Sonderfälle
Kap: Seite 5.1.4: S. 139 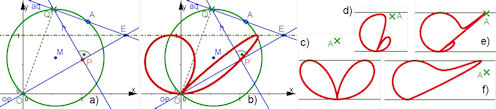Aufgabe 5.2		Abb. 5.4 In einem Streifen gefangenes Zweiblatt a) Konstruktion b) Zweiblatt c)-f) Das Zweiblatt mit anderen Lagen von Punkt A: c) (0,1.5) d) (0.4,0.9) e) (1.2,0.98) f) (2,0.5)
	im GeoGebra-Book download Aufgabe 5.2 gefangenes Zweiblatt
Kap: Seite 5.1.4: S. 141		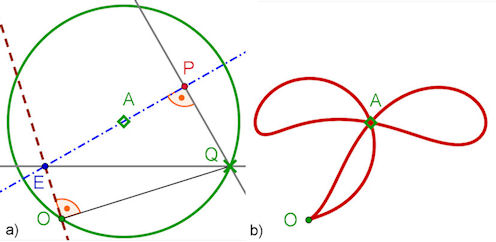Abb. 5.5 Zweikeimblatt im Wind Zu einem freien Punkt A wird Q zugfest auf einen Kreis um A durch den Ursprung O gesetzt. Die Senkrechte auf OQ in O schneidet die Parallele zur x-Achse durch Q in E. P ist der Fußpunkt des Lotes von Q auf die Gerade EA. Die Ortskurve von P bezüglich Q ist das Zweikeimblatt. im GeoGebra-Book download
	Bewegen Sie A frei in der Ebene. Überlegen Sie, warum das Zweikeimblatt nie aus seinem Erzeugungskreis herausragt. Liegt A auf der x-Achse, kommt eine Lemniskate heraus. Ist es die Lemniskate von Bernoulli (siehe Abschnitt 4.4.1)?
Kap: Seite 5.1.5: Zusatz		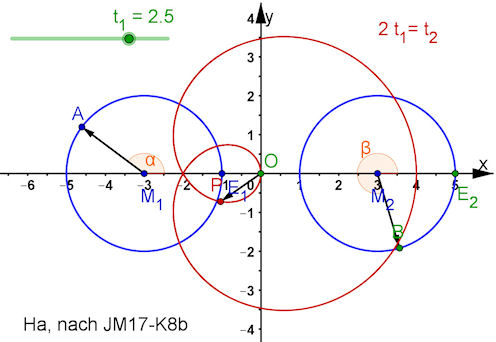Meyer'sche Kurven Dr. Jörg Meyer aus Hameln hat bei der Tagung des Ak Geometrie vorgeschlagen, in zwei Kreisen Zeiger mit verschiedenen Geschwindigkeiten laufen zu lassen. Der Summenvektor die Zeiger bestimmt das P für die Ortslinie. Dazu habe ich einiges Weitergehendes untersucht. Das ist hier noch nicht dargestellt. Zum Teil aber in der Mathematica-Datei zugreifbar. Mathematica-Notebook Meyer'sche Kurven Das Mathematica-Notebook zum Lesen

5.2 Frei erfundene Gleichungen und ihre Kurven
Kap: Seite 5.2: S. 141 Aufgabe 5.4		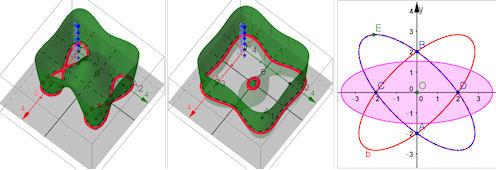Abb. 5.6 Isolierte Punkte als Sonderfall der Kurvenfamilie mit der Gleichung 5.1, wenn rechts statt der 0 eine Zahl n steht ( x^2 - a^2)^2 +(y^2 - b^2)^2 = 0 Afgabe 5.4 Isolierte Punkte und ihr Topf im GeoGebra-Book Topf download Ellipsen download

Kap: Seite 5.2.1: S. 143		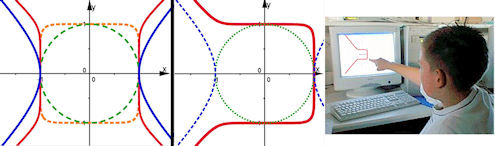5.2.1 Termsensibilisierung Abb. 5.7 Gleichungen von Kreis (grün) und Hyperbel (blau)variieren a) Exponenten 8 statt 2 ergibt Rundeckenquadrat und Platt-Hyperbel b) Hypellipse x^9 + y^8 = 1 c) Achtklässler zeigt seine Kreation a) download b) download

Kap: Seite 5.2.2: S. 143		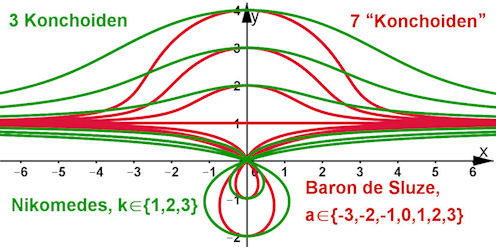Abb. 5.8 Echte Konchoiden des Nikomedes (y - b)^2(x^2 + y^2) = k^2y^2 (grün) b = 1, k ¸ {1, 2, 3} "Konchoiden" des Baron de Sluze (y - b)(x^2 + y^2) = a y^2 (rot) b = 1, a aus {-3,-2,-1, 0, 1, 2, 3} im GeoGebra-Book download

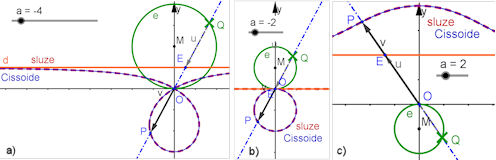
Kap: Seite 5.2.2 S. 144 Aufgabe 5.5		Aufgabe 5.5 Baron der Sluzes Familie als Cissoiden-Familie im GeoGebra-Book download

Kap: Seite 5.2.3: S. 145		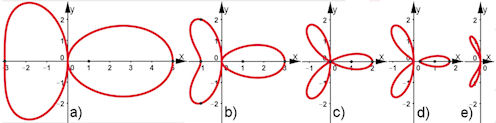Abb. 5.9 Wandelfisch aus gestörter Rosette: a) - e) Das s wird immer kleiner, bis bald alles verschwindet Wandelfisch offen download

Kap: Seite 5.2.3: S. 145		Abb. 5.10 Dem Wandelfisch hinter die „Kiemen“ geschaut: a) Elemente für die Diskussion der Eigenschaften, in b) und c) werden die explizit-kartesischen Bausteine sichtbar
	Wandelfisch beweise (noch nicht perfekt) Die Abb. 5.10 b) und c) sind mit Mathematica gemacht.