| 07 Kegelschnitte |
| Website zum Buch: Hier sind die Dateien, die die Bilder des Buches erzeugt haben, die Aufgabenlösungen, Beweis-Ergänzungen und weitere Kurven, für die im Buch kein Platz mehr war. Wenn Sie hier etwas nicht verstehen, lesen Sie im Buch. Falls Sie Fehler finden ober noch Fragen übrig sind, wenden Sie sich an mich. |
| 7.1 Einstieg |
7.2 Konstruktionen | 7.3 Dandelin |
7.4 Namensgeheimnis | 7.5 Reflexion | 7.6 Anwendungen | 7.7 Extras |
 7.1 Kegelschnitte, die berühmteste Kurvenfamilie | |||||||||||
| Kap: Seite 7.1: S. 182 |
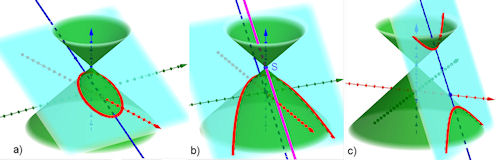
 im GeoGebra-Book alle download | Abb. 7.1 Ein Kegel wird von einer Ebene geschnitten. Die drei wichtigsten Schnittkurven
sind a) Ellipse, b) Parabel c) Hyperbel. Sonderfälle sind: Geradenkreuz, Doppelgerade als Mantellinie, einzelner Punkt. | |||||||||
| Kap: Seite 7.1.1: S. 182 |
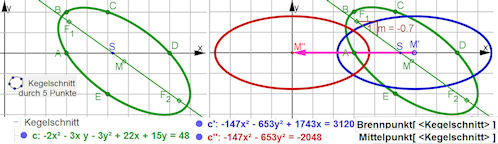 | Abb. 7.2 Ellipse aus 5 Punkten, sie wird passend gedreht und verschoben, so dass ihre Gleichung
als Mittelpunktsgleichung einer Ellipse erkennbar wird.
im GeoGebra-Book
download | |||||||||
| Kap: Seite 7.1.1: S. 184 |
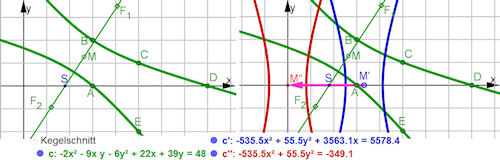 | Abb. 7.3 Hyperbel aus 5 Punkten, sie wird passend gedreht und verschoben, so dass ihre
Gleichung als Mittelpunktsgleichung einer Hyperbel erkennbar wird.
im GeoGebra-Book
download | |||||||||
| 7.1 Gemeinsame Konstruktionen | |||||||||||
| Kap: Seite 7.2.1: S. 186 |
a) im GeoGebra-Book
b) im GeoGebra-Book c) im GeoGebra-BookEllipse download
Parabel download
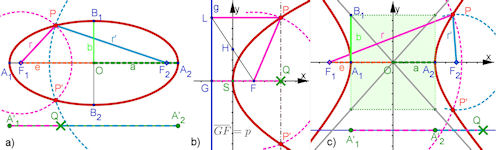
Hyperbel download | Abb. 7.4 Faden-Konstruktionen a) Ellipse: r + r' = 2a, b) Parabel: Strecke FP = Strecke LP, c) Hyperbel: |r -r'| = 2a | |||||||||
| Vokabeln: Hauptscheitel A1, A2, Hauptachse, grose Halbachse, Halbmesser a, Nebenscheitel
B1, B2, Nebenachse, kleine Halbachse, Halbmesser b, Brennpunkte F1, F2, F, Brennpunkteabstand
2e, Asymptoten der Hyperbel: graue Geraden, Steigung +/- b/a , Parabel: Leitgerade g und Strecke GF = p, Parabel-Parameter p. Die Zusammenhange werden im Text gezeigt. | |||||||||||
| Kap: Seite 7.2.2: S. 189 |
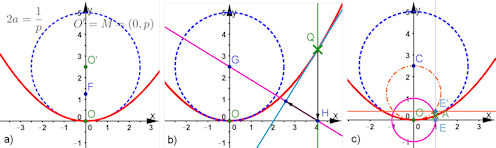
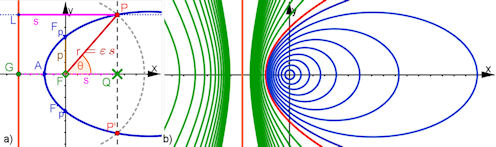 | Abb. 7.5 Leitgeraden-Konstruktion, konfokale Kegelschnitte a) Für den einzigen gemeinsamen Brennpunkt F wird der Ursprung gewählt. Die gemeinsame Leitgerade habe die Gleichung x = -g. Der Punkt Q auf der x-Achse bestimmt den Abstand s, den P von der Leitgeraden haben soll. | |||||||||
| Ein Kreis um F mit dem Radius epsilon mal s legt dann P fest.
b) Es ist g = 2 und die Kurven unterscheiden sich nur durch den Parameter epsilon. In 0.1-Schritten für epsilon entstehen Ellipsen, deren rechter Scheitel nach außen wandert. Ihr linker Scheitel rückt an(-g/2, 0) heran. Dieser Punkt ist der Parabelscheitel, die Parabel ist für epsilon = 1 die "Grenzkurve" der Ellipsen. Sowie aber epsilon > 1 wird, erhalten wir Hyperbeln. Ihre Scheitel bewegen sich (in 0.25-Schritten für epsilon) vom Parabelscheitel aus und von links auf die Leitgerade zu. | a) im GeoGebra-Book
a) Leitgeraden Konstruktion download
b) im GeoGebra-Book
b)Konfokale Kegelschnitte download | ||||||||||
| Kap: Seite 7.2.2: S. 190 |
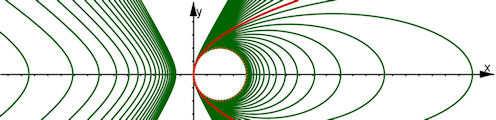 | Abb. 7.6 Kegelschnitte mit gemeinsamem Scheitel gemäß Formel 7.7 mit p = 1 und 0 < epsilon < 2 in 0.05-Schritten fuü epsilon.
im GeoGebra-Book
download
| |||||||||
| Es beginnt mit dem Kreis durch O mit dem Radius 1, es folgen Ellipsen, deren zweiter Brennpunkt (prinzipiell) ins Unendliche läuft, ohne zweiten Brennpunkt ist in Rot die Parabel y^2 = 2px hervorgehoben. Es folgen Hyperbeln, deren zweiter Ast "aus dem Unendlichen" von links mit Scheitel und Brennpunkt der y-Achse zustrebt. | |||||||||||
| Kap: Seite 7.2.2.1: S. 191 |
a) im GeoGebra-Book b) im GeoGebra-Book c) im GeoGebra-Book
Ellipse download
Parabel download
Hyperbel download
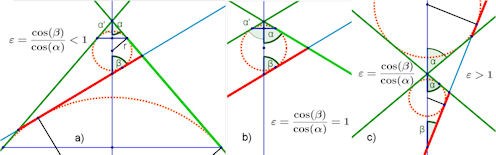
| Abb. 7.7 Numerische Exzentrizität epsilon, halber öffnungswinkel des Kegels alpha und Schnittwinkel beta der Ebene mit der Kegelachse, eingetragen sind in diesen Querschnitt auch die Dandelin'schen Kugeln aus Abschnitt 7.3. Für den Kreis ist epsilon = 0, denn beta = 90°, a) für andere Ellipsen ist 0 < epsilon < 1 , b) für die Parabel ist epsilon = 1, c) für Hyperbeln ist epsilon > 1. Dandelin'sche Kungeln in 3D | |||||||||
| Kap: Seite 7.2.3: S. 193 |
a) im GeoGebra-Book b) im GeoGebra-Book
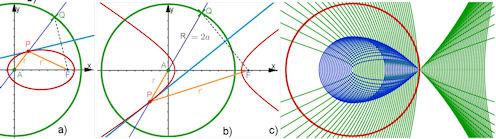
a) download b) download | Abb. 7.8 Kegelschnitte aus der Leitkreis-Konstruktion: Q ist zugfest auf einem Kreis um A
mit dem Radius 2a. Zu F = (2e, 0) und Q wird die Mittelsenkrechte gezeichnet. Sie schneidet die
Radiusgerade AQ in P. Die Ortslinie von P ist ein Kegelschnitt. Die hellblaue Mittelsenkrechte
wird Tangente. a) Ellipse, man sieht die Fadenkonstruktion: AP+PF = AP+PQ = AQ = 2a. b) Hyperbel entsprechend: FP -PA = QP -PA = AQ = 2a. | |||||||||
| c)Konfokale Kegelschnitte: Brennpunkt A und der rote Leitkreis sind fest. F rückt in kleinen Schritten nach rechts. Die blauen Ellipsen werden flacher und „springen“, wenn F den Leitkreisrand überschreitet, in die grünen Hyperbeln über. |
c)im GeoGebra-Bookc)mit Spur download | ||||||||||
| 7.3 Beweise mit den Dandelin'schen Kugeln | |||||||||||
| Kap: Seite 7.3: S. 194 |
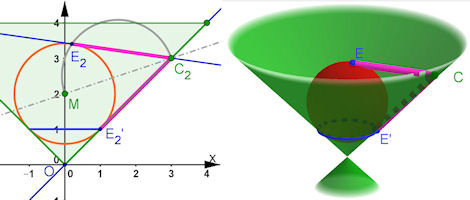 | Abb. 7.9 Grundlage für die
Dandelin’schen Kugeln
Merke: Legt man von einem Punkt
aus Tangenten an eine Kugel, sind
die Tangentenabschnitte gleich
lang. Merke: Eine Kugel, die in
einem Kegel steckt, berührt ihn
längs eines Kreises, dessen Ebene
senkrecht auf der Kegelachse
steht.
| |||||||||
| Kap: Seite 7.3.1: S. 44 |
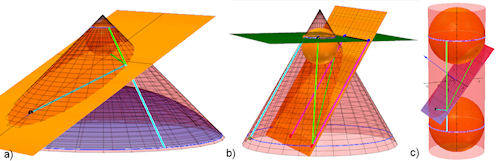 | Abb. 7.10 Dandelin’sche Kugeln a) Für die Ellipse als Kegelschnitt, b) für die Parabel als Kegelschnitt, c) für die Ellipse als Zylinderschnitt. Gezeigt im Querschnittin Abb.7.7 Übersicht mit den drei Bildern 
| |||||||||
| |||||||||||
| 7.3 Namensgeheimnis der Kegelschnitte | |||||||||||
| Kap: Seite 7.4: S. 196 |
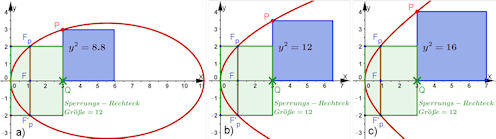 | Abb. 7.11 Namensgeheimnis der Kegelschnitte Q ist zugfest auf der Achse, an derselben Abszisse x ist P auf dem Kegelschnitt mit der Ordinate y. Griechisch: elleipein = ermangeln, zu wenig sein paraballein= gleichkommen, gleich sein hyperballaein= übersteigen, mehr sein | |||||||||
| Das Sperrungs-Rechteck (grün) hat die Breite x und als Höhe die Sperrung 2 · p (Def. 7.3). Es wird also vom Scheitel, von Q und der Ordinate von Fp, nämlich p festgelegt. Im Bild ist einheitlich p = 2 und x(Q) = 3. Das Sperrungs-Rechteck hat dann die Fläche 2 · 2 · 3 = 12, allgemein 2px. Es wird mit dem Ordinatenquadrat y^2 (blau) an der Stelle x verglichen: a) Für die Ellipse ist y^2 < 2px, b) für die Parabel ist y^2 = 2px, c) für die Hyperbel ist y^2 > 2px. im GeoGebra-Book
im GeoGebra-Book
im GeoGebra-Book
Ellipse download
Parabel download
Hyperbel download
| |||||||||||
| 7.5 Reflexion und Tangenten an den Kegelschnitten | |||||||||||
| Kap: Seite 7.5.1: S. 198 |
 | Abb. 7.12 Tangenten, Normalen an den Kegelschnitten:A und F sind Brennpunkte des Kegelschnittes Diese Dateien sind in Abschnitt 7.5.3 nochmals aufgegriffen zund werden da für die Reflexion genutzt. | |||||||||
| a)im GeoGebra-Book
b) im GeoGebra-Book
c) im GeoGebra-Book
Ellipse download
Parabel download
Hyperbel download
Ellipse und Hyperbel haben als zweiten Brennpunkt A. Q ist zugfest auf dem Leitkreis bzw. der Leitgeraden. Die Mittelsenkrechte (hellblau) von Strecke FQ wird im Text als Tangente nachgewiesen. Die Normale als Senkrechte auf der Tangente ist durch Strichpunkte gekennzeichnet. Sie ist parallel zu der anderen gestrichelten Strecke. An diesen Parallelen kommt der Winkel PQF wegen der Mittelsenkrechten auch als Winkel QFP und als Stufenwinkel Winkel(r, Lot) vor. Als Wechselwinkel von QFP hat auch Winkel(Lot, r) diese Größe. Damit ist direkt die Reflexion eines Strahles von A an P nach F dargestellt. Bei der Parabel ist der zweite Brennpunkt A ins Unendliche gerückt, wir nehmen ersatzweise A˜ aus QP rechts (s. Abschnitt 7.2.3). Auch bei der Hyperbel hilft uns A˜aus QP auf der rechten Seite. Die Winkelbetrachtung gilt dann für alle Fälle. | |||||||||||
| Kap: Seite 7.5.1.2: S. 200 |
 im GeoGebra-Book
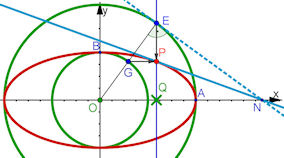download | Abb. 7.13 Scheitelkreis-Konstruktion der
Ellipse mit Tangentenkonstruktion Die grünen
Kreise heißen Hauptscheitelkreis und Nebenscheitelkreis.
Die Ortskurve von P ist die Ellipse x^2/a^2+y^2/b^2=1. Die Tangente in P erhält man, indem man die Senkrechte auf dem Radius OE mit der x-Achse schneidet und mit dem so erhaltenen Punkt N die Gerade NP bildet. | |||||||||
| Kap: Seite 7.5.1: S. 201 |
im GeoGebra-Book
download
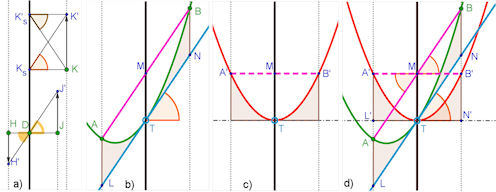
| Abb. 7.14 Tangenten und Sehnen bei der Parabel:
a) Scherung pur, b) Eine Parabel mit Sehne AB und deren Mitte M. Es ist T der Parabelpunkt mit derselben Abszisse wie M. Die Tangente in T ist parallel zur Sehne AB. Der Beweis erfolgt durch die Scherung von Bild b) zu Bild c): Das Parallelogramm LNBA ist geschert zum Rechteck L'N'B'A'. Bei diesem ist die Parallelität von Sehne und Tangente in T trivial. Wegen der Flächentreue ist auch die Fläche zwischen Parabel und Tangente in b) genauso gros wie in c), also 1/3 des Vierecks, wie man aus Analysis weis. d) Hier sind b) und c) gemeinsam dargestellt und man kann die Scherung mit den Augen besser nachvollziehen. | |||||||||
| Kap: Seite 7.5.3: S. 202 |
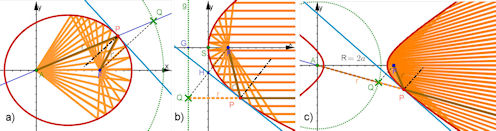 | Abb. 7.15 Reflexion an den Kegelschnitten: Die Strahlenbüschel sagen im Vergleich zu
Abb. 7.12 nichts Neues aus, sie zeigen nur die Reflexion eindrucksvoller. Daher nochmals: Beachten, dass Sie "Spur" hinzuschalten können. | |||||||||
|
a)im GeoGebra-Book
b) im GeoGebra-Book
c) im GeoGebra-Book
Ellipse download
Parabel download
Hyperbel download
| |||||||||||
| 7.6 Anwendungen der Kegelschnitte | |||||||||||
| Kap: Seite 77.6.1: S. 204 |
 | Abb. 7.16 Parabeln im Kurpark Man setzt drei Punkte A, B, C auf einen Bogen und wählt
dann in GeoGebra Polynom[A,B,C]. In der hier sinnvollen Genauigkeit passen die Parabeln.
download | |||||||||
| Kap: Seite 7.6.1: S. 205 |
 | Abb. 7.17 Kanalbrücke
als Parabel Zu dem Bild in GeoGebra wird mit Schiebereglern k, a und b die Parabel y = k (x - a)^2 + b definiert, an die richtige Stelle geschoben und die Öffnung experimentell bestimmt. im GeoGebra-Book
download
| |||||||||
| Kap: Seite 7.6.1: S. 205 |
 | Abb. 7.18 Berlin: a) Die Reichstagskuppel ist ein halbes Ellipsoid und keine Halbkugel, das weiße Kreuz ist der Brennpunkt, er liegt weit ab von der Mitte. b) Die Öffnung des Berliner Hauptbahnhofs ist eine halbe Ellipse. | |||||||||
| a) im GeoGebra-Book
Reichstag download
b) im GeoGebra-Book
Bahnhof download
| |||||||||||
| Kap: Seite 7.6.1.1: S. 206 |
a)im GeoGebra-Book
a) Planet und Impulssatz download
b) im GeoGebra-Book
b) Planet und Flächen download (weiter rechts)
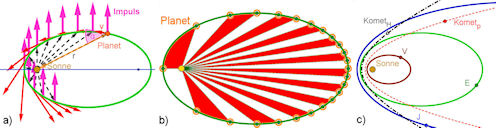
| Abb. 7.19 Kepler’sche Gesetze a) Nach dem 1. Gesetz ist die Bahn ist elliptisch und der Grund für das 2. Gesetz ist, dass der Drehimpuls (violett) vektor(i)= m vektor(r) × vektor(v) = konstant ist. Dabei steht senkrecht auf der Bahnebene. b) Visualisierung des 2. Gesetzes: Alle roten und weißen Segmente haben dieselbe Fläche und der Planet braucht auf seiner Bahn für jedes Segment dieselbe Zeit. Also ist in Sonnennähe (perihel) die Bahngeschwindigkeit des Planeten größer als in Sonnenferne (aphel). In der Datei für b) sind schwierigere Analysisprobleme vollständig mit GeoGebra geläst: Algebra,CAS und zwei Graphikfenster sind sinnvoll verwendet. Für diesen Zusammenhang gibt es inzwischen eine gute interaktive Version in GeoGebra, genauer Link  https://masuv.web.leuphana.de/!!hoema/01Ana2d/01.8Integral.htm#kepler
in dem neuen Buch 
| |||||||||
|
im GeoGebra-Book c) Planet und Kometen download
c) In einem Planetensystem hängen die elliptischen Bahnen und die Umlaufzeiten über das 3. Kepler’sche Gesetz zusammen. Das gilt auch für manche Kometen. Andere kommen mit so hoher Energie aus dem Weltall, dass sie nicht „eingefangen“ werden. Sie werden auf hyperbolischen Bahnen umgelenkt. Eine Parabelbahn ist möglich, aber sehr unwahrscheinlich. (Darstellung nicht maßstabsgerecht.) Ergänzt: Zu der Epizykeltheorie von Apollonius Epizykel download
| |||||||||||
| Kap: Seite 7.6.2: S. 208 |
 | Abb. 7.20 Parabolrinnen im Solarkraftwerk Anasol in Andalusien, das parallele Sonnenlicht
wird zu der Brenngeraden reflektiert, dort wird maximale Energie abgegriffen. (Quelle:
www.solarMillennium.de)
| |||||||||
| Kap: Seite 7.6.2: S. 208 |
 | Abb. 7.21 Flüstern weit
entfernt hören:
a) Flüsterbogen in Görlitz, Untermarkt 12, b) Flüstergewölbe im Kloster c) Flüsterschalen im Technik-Museum Berlin | |||||||||
| Kap: Seite 7.6.3: S. 210 |
 | Abb. 7.22 Projektionen im Verkehr Wenn Fahrradwege einmünden (schwarz) oder queren (rot) ist manches Mal ein Bild eines Fahrrades als Bodenmarkierung angebracht. Das rote Bild ist senkrecht von oben fotografiert, Boden und Bildebene sind parallel. Da hat das Fahrrad stark elliptische Räder. Aber im schwarzen Bild ist gezeigt, dass diese aus Sicht des Verkehrsteilnehmers ganz „normal“ kreisrund erscheinen. Das gelbe untere Bild ist auf einem Umleitungsschild für einen Fahrradweg. Setzt man die Kamera auf das Schild, so sind wieder Urbild- und Bildebene senkrecht aufeinander: aus dem Kreis wird eine Ellipse. | |||||||||
| Kap: Seite 7.6.3: S. 210 |
 a)im GeoGebra-Book b) im GeoGebra-Book c) im GeoGebra-Book
a) Ellipsen download
b) Konstruktiver Zusammenhang 3D download
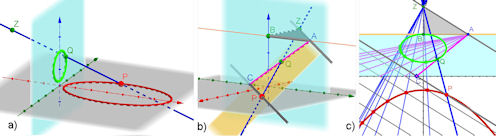c) dieselbe Konstruktion in 2D (Lietzmann/Lambert) download | Abb. 7.23 Projektion von Ellipse und Parabel a) Ein Kreis wird i. d. R. auf eine Ellipse projiziert, b) Konstruktiver Zusammenhang von Punkt Q und Bildpunkt P oder umgekehrt im Raum, c) derselbe Zusammenhang, nun konstruierbar in einer 2D-Darstellung, nach [Lietzmann 1933] und [Lambert 2016](im Mathematik-Lehren). Gezeigt ist der Zusammenhang zwischen einer Parabel in der x-y-Ebene und einer Ellipse, welche die Horizontgerade BA berührt. Erläuterungen erfolgen im Text. Lambert schlägt eine unterrichtliche Umsetzung mit gefalteter Pappe vor. | |||||||||
| 7.7 Extras und Aufgaben | |||||||||||
| Kap: Seite 7.7.1: S. 212 |
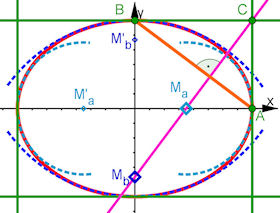 Man verbindet Hauptscheitel A und Nebenscheitel
B und fällt vom Punkt C = (a, b) das
Lot auf diese Strecke. Es schneidet die x-Achse in
Ma und die y-Achse in Mb. Es sind R = Ma A und
r = Mb B schon die Radien der Krümmungskreise
in A und B. Der nächste Abschnitt zeigt:
R = b^2/a und r = a^2/b.
|
Abb. 7.24 Scheitel-Krümmungskreise der
Ellipse: Diese Beziehungen werden
wirklich konstruiert: Das violette Lot durch C hat
als Senkrechte auf AB die Steigung m = a/b = b/R und m = a/b= r/a.
im GeoGebra-Book
Ellipse download
| |||||||||
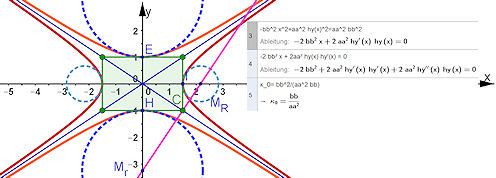
| Kap: Seite 7.7.1: S. 212  7.1 |
 | Afg.7.1 Krümmungskreise der Hyperbel und der Parabel
Hyperbel im GeoGebra-Book
Hyperbel download
Parabel a) und c) download
Parabel b) download
| |||||||||
| Kap: Seite 7.7.2: S. 213 7.2 |
 a) 2 Kreis-Systeme download
b)Kreis-System +Parallelenschar download Zwei Vorlagen als -Seite
Aufgabe 7.2 Raster mit Kreis- und Parallenenscharen
a)und Afg7.2-1 a)+b), Afg7.2-5 download b) und Afg7.-2, download b) und Afg7.-3, download
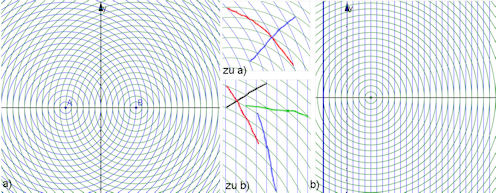b) und Afg7.-4, download | Abb. 7.25 Die Rastervorlagen für Kegelschnitte zum Selberzeichnen,
a) Zwei Scharen konzentrischer Kreise. Zeichnen Sie, wie in der Mitte oben vorgemacht, Diagonalenfolgen durch die kleinen Quasi-Rauten. Zeichnen Sie viele Kurven. b) Eine Schar konzentrischer Kreise um einen Punkt. Dazu ist eine Parallelenschar gezeichnet. Probieren Sie die Zeichenvorschäge in der Mitte unten aus. | |||||||||
Afg7.2 im Mathematica- Notebook
Das Mathematica-Notebook zum Lesen | |||||||||||
| Kap: Seite 7.7.2: S. 215 7.3 |
 |
Afg.7.3 Konfokale Kegelschnitte
Zum Bild links
Zu 3. Reflexion
Zu 4., gemeinsames b
| |||||||||
|
Aufgabe 7.3 Konfokale Kegelschnitte
Das Mathematica-Notebook zum Lesen
| |||||||||||
| Kap: Seite 7.7.2: S. 215 7.4 |
 |
Aufgabe 7.4 Konjugierte Richtungen
a)download
b)download
c)download
| |||||||||
| Kap: Seite 7.7.2: S. 215 7.5 |
b)im GeoGebra-Book
b)Bezierkurve pur download
Parabel als Vorstufe zu Bézierkurven |
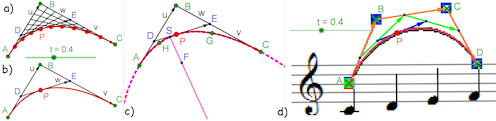
Abb. 7.26 Das Prinzip der Bézier-Kurven, a)-c) in einer Vorstufe, d) in der „echten“ Form. d) im GeoGebra-Book
 d)Bezierkurve mit Notenbogen download
| |||||||||
|
Für c): Erzeugen Sie mit "Kegelschnitt durch 5 Punkte" die Kurve und überzeugen Sie sich mit Scheitel[] und Brennpunkt[] und dann Parabel aus Scheitel und Brennpunkt, dass es eine Parabel ist.
c)Bezierkurve mit Parabeltest download Bezierparabel mit Bernsteinpoynomen exakt gerechnet und gedreht, statisch
Bezierparabel als Parameterkurve mit Bernsteinpoynomen exakt gerechnet, dann t eliminiert und nach obiger statischen GeoGebra-Datei übetragen
dasselbe zum Lesen für alle
Bezierparabel als Parameterkurve mit Bernsteinpoynomen exakt gerechnet und gedreht, dynamisch
| |||||||||||
| Kap: Seite 7.7.2: S. 216 7.6 |
 | Aufgabe 7.6 Pol und Polare bei Kegelschnitten
Zu a) download
Zu b) download
Zu c) download
Zu d) download
| |||||||||
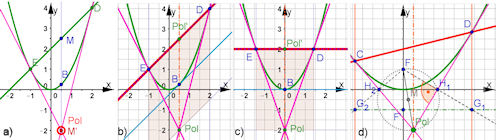| Kap: Seite 7.7.2: S. 215 7.7 |
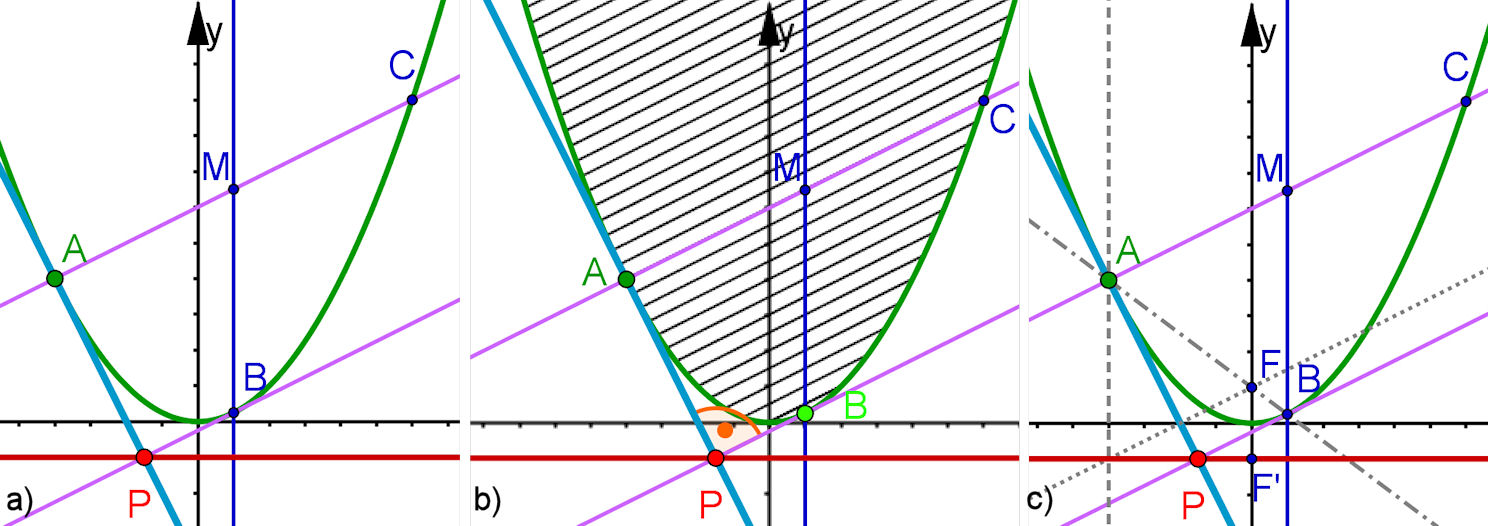
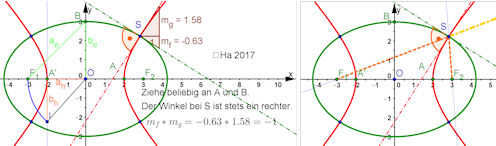
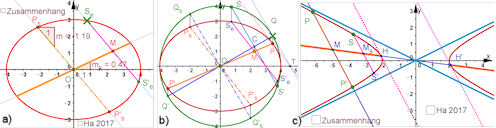
Im Lösungstext Abb. 7.11 Orthoptische Kurven zu Ellipsen und Hyperbeln a) Die Normale definiert eine Sehenschar, deren kongugierter Durchmesser den Punkt B liefert. Die orthoptische Kurve der Ellipse besteht aus zwei Kreisbögen, b) ebenso erhält man mit der Geraden durch die Sehenmittelpunkte und den Ursprung nun zwei Punkte B1 und B2 auf den beiden Ästen. Die Schnittpunkte der Tangenten zu A und B1 beziehen sich auf den Ast von A, die von A und B2 auf verschiedene Äste. Die orthoptische Kurve der Hyperbel besteht aus je zwei Kreisbögen, die sich zu einem Kreis ergänzen. | Aufgabe 7.7 Orthoptische Kurven zu Kegelschnitten
Im Lösungstext Abb.7.10 Orthoptische Kurve zur Parabel a) Konstruktion mit der Normalen, b) Zusammenhang mit den konjugierten Durchmessern, c) Begründung mit den geometrischen Parabeleigenschaften und dem Brennpunkt F im GeoGebra-Book
Zu Parabel download
Zu Ellipse download
Zu Hyperbel download
Mathematica-Rechnungen dazu
Das Mathematica-Notebook zum Lesen
| |||||||||
| Kap: Seite 7.7.2: 217 7.8 |
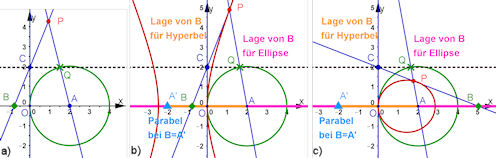
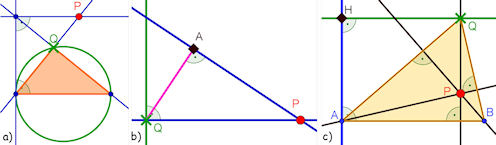 | Abb. 7.27 Orte erkunden, stets wandert Punkt Q zugfest auf seinem grünen Weg, auf die
gezeigte Weise entsteht Punkt P, dessen Ortslinie gesucht ist.
Aufgabe 7.8 Elementare Ortsaufgaben
Weitere Beispiele in der Lösung. | |||||||||
| a) im GeoGebra-Book b) im GeoGebra-Book c) im GeoGebra-Book
a) Kreisweg für Q download
b) Geradenweg für Q download
c)Höhenschnitt download
| |||||||||||
| Kap: Seite 7.7.2: 218 |
a) im GeoGebra-Book b) im GeoGebra-Book c) im GeoGebra-Book
a)download
b)Kreuz download
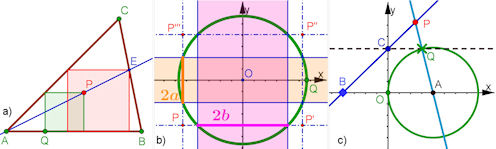
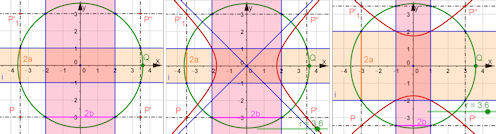
c)drei ??? download | Abb. 7.28 Ortsaufgaben a) Das einbeschriebene Quadrat findet man mit einer Ortslinie. b) Das breite Kreuz wird von einem Kreis mit variablem Radius geschnitten. Gesucht ist der geometrische Ort der vier symmetrisch gelegenen Punkte P, P', P'', P'''. c) Die drei ??? erscheinen unvermutet als Ortskurven von P bezüglich Q, wenn man drei wesentliche Stellungen von B betrachtet. | |||||||||
| Kap: Seite 7.7.2: S. 218 7.9 |
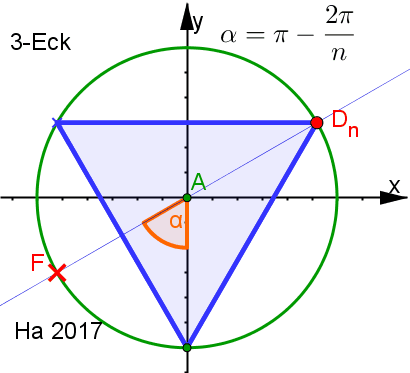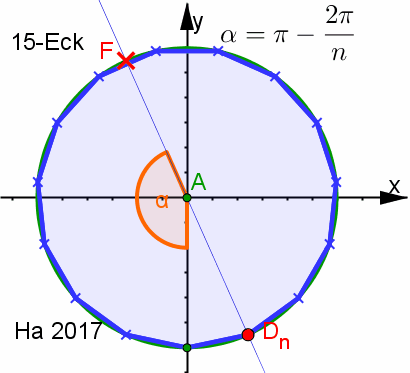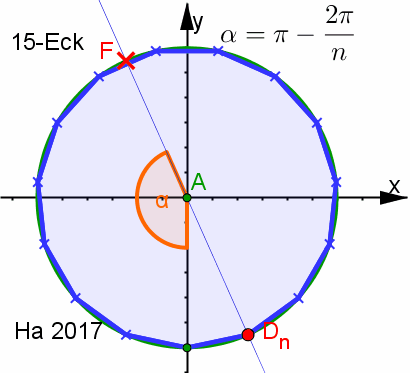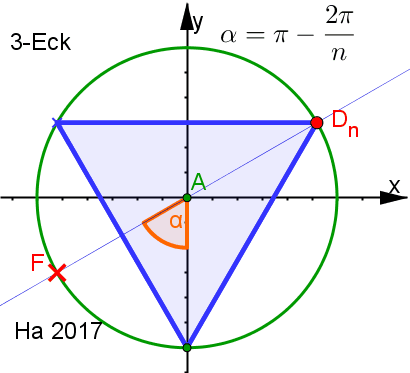
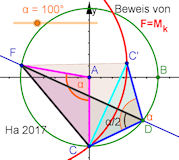
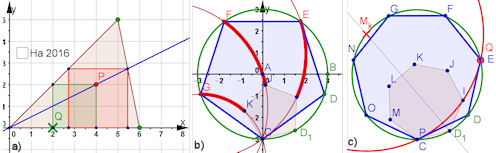 | Aufgabe 7.9 Quadrat im Dreieck, Zusatz: 5-Eck erkunden, 7-Eck "konstruieren" Darin Beweis für alle n-Ecke. | |||||||||
a)Dreieck download b) 5-Eck erkunden c) 7-Eck "konstruieren"
 
n-Eck Beweis für den Start
Animierte dynamische Version | |||||||||||
| Kap: Seite 7.7.2: S. 217 7.10 |
 | Aufgabe 7.10 Das breite Kreuz
im GeoGebra-Book
download
| |||||||||
| Kap: Seite 7.7.2: S. 218 7.11 |
 | Aufgabe 7.11 Die drei ??? (Fragezeichen) tauchen auf
im GeoGebra-Book
Aufgabe pur download
Lösung download
Mathematica-Notebook
Das Mathematica-Notebook zum Lesen
| |||||||||
 Prof. Dr. Dörte Haftendorn |
Erstellt August 2016, Update |
www.kurven-erkunden-und-verstehen.de |
 | ||
Lernseite Ellipse und Parabel