|
 9.1 Fußpunktkurven | |||
| Kap: Seite 9.1: S. 255 |
 | Siehe Abb.8.22 Fußpunktkurve der Astroide Siehe Abb.8.9c in Blau Fußpunktkurve der Königin der Spiralen | |
| Kap: Seite 9.1.1.1: S. 256 |
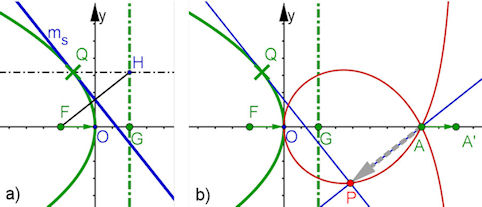 | Abb. 9.1 Parabel a) Parabel y^2 = -2p x mit Brennpunkt und Leitgerade in Grun. Lot und Tangente als Mittelsenkrechte (blau), b) dazu der Pol A = (a, 0) und die Fuspunktkurve als Ortskurve von P bezüglich Q. Die Asymptote steht bei A'. Der graue Pfeil kommt erst später zum Einsatz.  im GeoGebra-Book
download
| |
Beim Aufstellen der Gleichung muss es heißen  , denn die Steigungen von Tangente und Lot müssen das Produkt -1 haben. Es war nur ein Schreibfehler, die nachfolgende Formel ist richtig. Als Wiedergutmachung ist hier die Herleitung "von Hand" und auch die mit Mathematica gezeigt. 
Mathematica-Notebook
Das Mathematica-Notebook zum Lesen
| |||
| Kap: Seite 9.1.1.4: S. 260 |
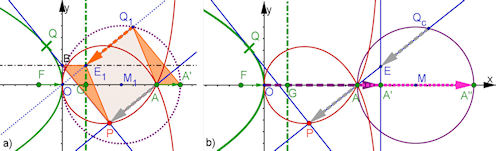 | Abb. 9.2 a) Beweisfigur, b) Cissoidenkonstruktion
Dieselbe Datei wie zu Abb. 9.1 im GeoGebra-Book
download
| |
| Kap: Seite 7.7.2: S. 215  9.1 |
 |
Aufgabe 9.1 Sluze-Kurven als Fußpunktkurven der Parabel
Sluze-Parabelpedal download
Animierbar, links
Animierbar, rechts
| |
| |||
| Kap: Seite 7.7.2: S. 215 9.29.3 |
  |
Aufgabe 9.2 Pedale der Ellipsen
Aufgabe 9.3 Pedale der Hyperbeln
Pedal-Kegelschnitte Für Hyperbeln in der Kegelschnittgleichung + durch - esetzen.
Pedalkurven der Ellipse, Gleichung
Pedalkurven der Hyperbel, Gleichung
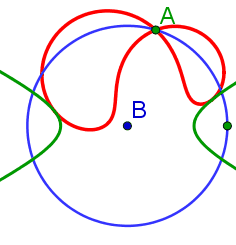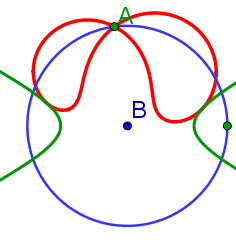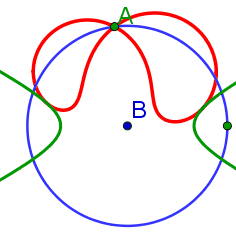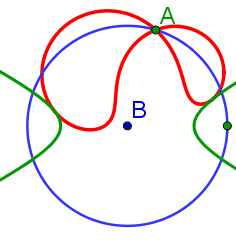Herleitung der allgemeinen Pedalgleichung für Ellipsen und Hyperbeln
Mathematica-Notebook
Das Mathematica-Notebook zum Lesen
Beweiszeichnung für den Satz: alle Pascal'schen Schnecken sind Pedalkurven eines Kreises und umgekehrt.
Ellipse animierbar
Hyperbel animierbar
| |
| Kap: Seite 9.1.2: S. 262 9.4 |
 
im GeoGebra-Book
download
| ||
| |||
  afg9.4-pedal-astroide.cdf ( Info zum Mathematica-Player)
| Teil-Aufgabe 9.4 Pedalkurven der Astroide
Astroide und ihre Pedalkurven, download
Mathematica-Notebook
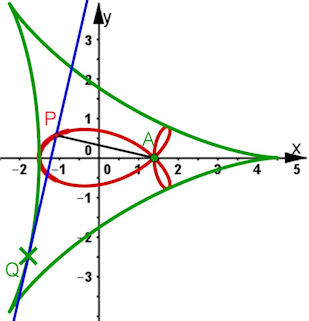
Klicken Sie den Button enable dynamics, wenn's mal nicht losgeht.
Das Mathematica-Notebook zum Lesen
Hier stehen auch alle Berechnungen und Beweise. Für das linke Bild siehe auch Kap. 8.2.2 S. 240 im GeoGebra-Book
Astroide und Quadrifolium als Pedalkurve, download
| ||
| Kap: Seite 9.1.3: S. 263 |
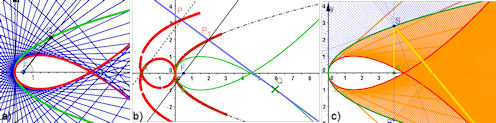
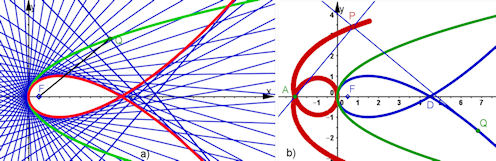  | Abb. 9.4 a)Tschirnhaus-Kubik als negative Fußpunktkurve der Parabel, Pol A ist der Brennpunkt F. b) In Rot ist eine Fußpunktkurve der Tschirnhaus-Kubik gezeigt. Wo muss A stehen, damit die Parabel wieder herauskommt? a) im GeoGebra-Book
a) download
b) im GeoGebra-Book
b) downloadEtwas anders gebaut, damit die rote Kurve als Ortslinie erscheinen kann. Unten nochmal "echt" konstruiert. | |
| Aufgabe 9.5 Fußfunktkurven der Tschirnhaus-Kubik
b) "Echte" Konstruktion mit Q auf der Kubik
c) Tschirnhaus-Kubik als Kaustik der Parabel
| ||
| Kap: Seite 7.7.2: S. 215 Afg9.5 |
 |
Aufgabe 9.5 Pedalkurven der Tschirnhaus-Kubik
Ergänzung: zweiter Teil: Betrachtung beliebiger Pole.
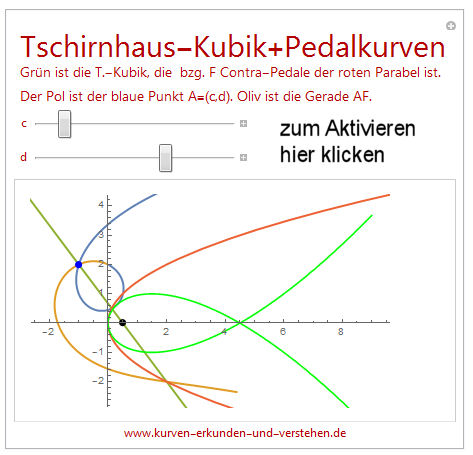Interaktiv mit Mathematica CDF-Datei direktInfo zum Mathematica-Player
Mathematica-Notebook
Das Mathematica-Notebook zum LesenHier stehen auch alle Berechnungen und Beweise. | |
| 9.2 Enveloppen, Evoluten, Involuten, Evolventen | |||
| Kap: Seite 9.2.: S. 264 |
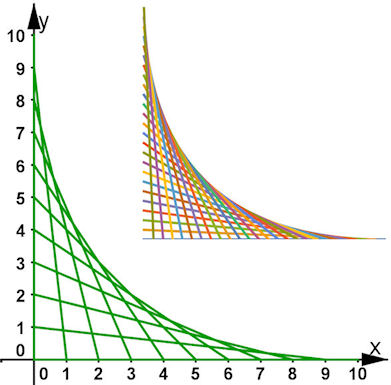 | Abb. 9.5 Naum-Gabo-Kurven In diesem Bild sind die Achsen gleichmäßig eingeteilt und entsprechende Punkte verbunden. Wenn wir den y-Achsenabschnitt t nennen, dann ist die Steigung der grünen Geraden m = - t/( a-t) . Dabei ist hier a = 10, die Länge des ersten und des letzten Fadens. Die Gleichung der grünen Geraden ist damit y = - t( a-t) x + t oder in anderer Schreibweise: F(x, y, t) = t x + (a - t)(y - t) = 0 Formel(9.8) Die Kurvenschar mit einer solchen Standardform der Kurvengleichung
(siehe Satz 2.1) zu beschreiben, bewährt
sich beim Umgang mit Hüllkurven.
| |
| Kap: Seite 9.2.3: S. 268 |
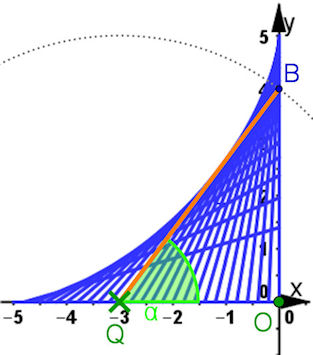
 | Abb. 9.6 a) Q ist zugfest auf der x-Achse. Auf Strecke FQ steht in Q eine Gerade senkrecht. b) Die Spur der Geraden bei Bewegung von Q zeigt eine Hüllkurve c) Zur Berechnung mit der Extremum-Methode sucht man bei festem x die „höchste“ Gerade. | |
| Diese Konstellation ist auch als "Das rutschende Geodreieck" bekannt im GeoGebra-Book
download
| |||
| Kap: Seite 9.2.4: S. 269 |
 
im GeoGebra-Book
download
| ||
| 9.3 Evoluten als Hüllkurven von Normalenscharen | |||
| Kap: Seite 9.3: S. 271 |
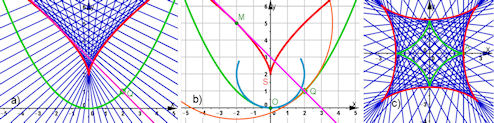 | Abb. 9.8
a) Normalenschar und Evolute der Parabel, b) Die Evolute ist nicht nur Hüllkurve der Normalenschar, sondern auch Kurve der Krümmungskreis-Mittelpunkte, c) Normalenschar und Evolute der Astroide a) im GeoGebra-Book
a) download
b) download
c) im GeoGebra-Book
c) download | |
| Parabel y=1/4 x^2, Evolute der Parabel ist eine Neil'sche Parabel, siehe Die Ortskurve aller Krümmungskreis-Mittelpunkte ist die Evolute. Die Astroide hat eine genau umfassende Astroide als Evolute. | |||
| Kap: Seite 9.3.3: S. 273 |
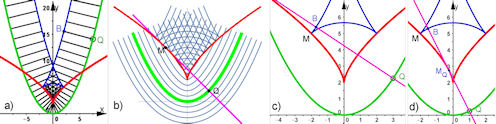 | Abb. 9.9 Evolventen und Paralelkurven a) Eine Parallelkurve der Parabel im festen Abstand BQ und ihr Zusammenhang mit der Evolute der Parabel (rot), b) Parabel (grün) mit ihrer Evolute und deren Evolventen, die auch Parallelkurven der Parabel sind, c) und d) Konstellation aus Abb. 9.8 b) zum Verstehen der gespitzten Abwickelkurven (Evolventen) in Bild b) links | |
| a) im GeoGebra-Book
a) download
b) download c)im GeoGebra-Book c) download
| |||
| Zusatz |  Aufgabenstellung und Diskission 
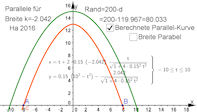|  Berechnung der Parallelkurve zu 9.3.3.1 Seite 299 und Integral einer Parameterkurve | |
|
Halle 1 download Halle 2 download Halle 4 download Halle 5 download
| |||
| Kap: Seite 9.3.3.1: S. 274 |
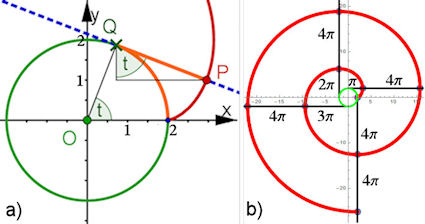 | Abb. 9.10 Kreis-Evolvente
a) Zeichnung zur Begrundung der Parameterdarstellung (Erklärung im Text): x(t)=a cos(t) + a t sin(t) y(t)=a sin(t) - a t cos(t) (9.15) b) Der vom Kreis mit a = 2 abgewickelte Faden ist markiert für t = n pi/2. a) im GeoGebra-Book
a) download
b) download
| |
| Kap: Seite 9.3.3.2: S. 274 |
 | Abb. 9.11 Die Kreis-Evolvente nähert sich einer
um pi/2
zuruck gedrehten archimedischen Spirale.
a) Das Rechteck OQPPA führt auf Strecke OPA = r(theta) = a t = a (theta+ pi/2) ). Diese archimedische Spirale ist violett eingezeichnet. b) Die Annäherung ist schon nach der Abwicklung von einem Kreisumfang recht gut. Dieselbe Datei wie b) von Abb.9.10 b) download
| |
| 9.4 Reflexion und Kaustiken | |||
| Kap: Seite 9.4.1: S. 276 |
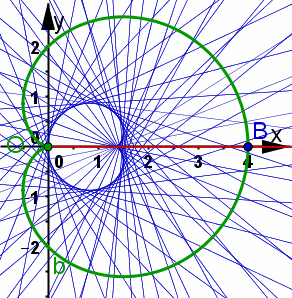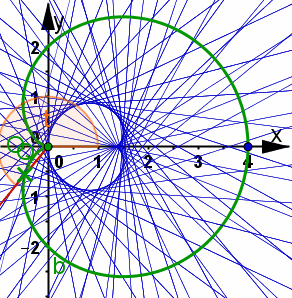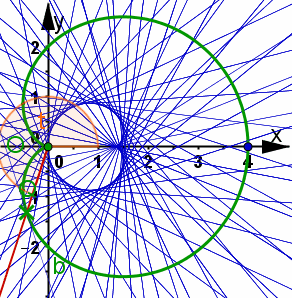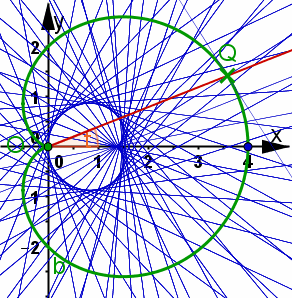
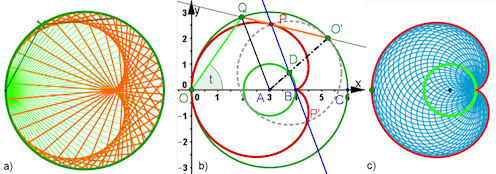 | Abb. 9.12 a) Kardioide als Katakaustik, b) Kardioide als passende Pascal’sche Schnecke (Limaçon) mit A = (a, 0), c) Kardioide als Hüllkurve von Kreisen um Punkte des grünen Kreises. Der Beweis in der Mitte ist bemerkenswert: Erst durch das Verwiklichen beider Konstruktionen in GeoGebra kommt man auf den entscheidenden Beweisgedanken. Siehe Text im Buch | |
| a) im GeoGebra-Book
a) download
b) im GeoGebra-Book
b) download c) im GeoGebra-Book
c) download
| |||
| Kap: Seite 9.4.1.6: S. 279 9.6 |
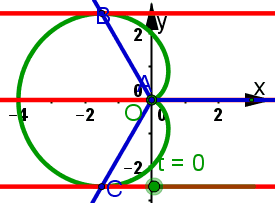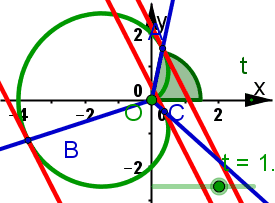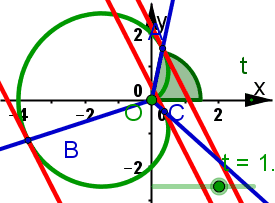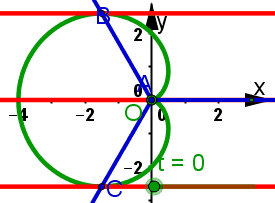 Animiertes BildSeite neu laden, wenn es sich nochmals bewegen soll. Firefox Stgr R IE Stgr R Goolgle Chrome Re Maus, Frame neu laden 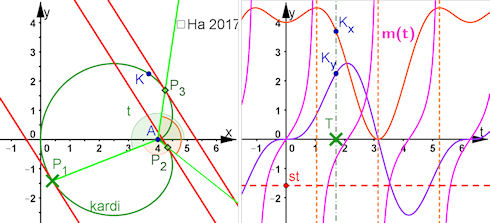 | KardioideAufgabe 9.6 Die drei Tangenten In dieser Lösung zu Aufgabe 9.6 sind Rechungen zu beiden Stellungen und ausführliche Erkärungen zum nachfolgenen Bild. Datei zu dem animierten Bild
Aufgabe 9.6 Die drei TangentenIn dieser Lösung zu Aufgabe 9.6 sind Rechungen zu beiden Stellungen und ausführliche Erkärungen zum linken Bild. Datei zu der Lage im linken Bild mit Erklärungen
Mathematica-Notebook
Das Mathematica-Notebook zum Lesen
| |
| Kap: Seite 9.4.1.6: S. 279 9.7 |
 
Aufgabe 9.7 Evolute der Kardioide
obiges download
Mathematica-Notebook
Das Mathematica-Notebook zum Lesen
| ||
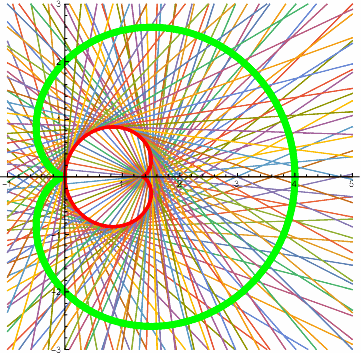
| Kap: Seite 9.4.2: S. 280 |
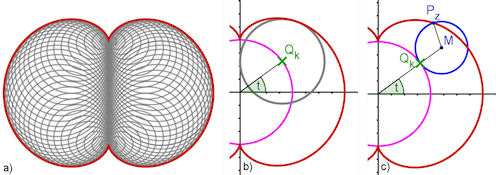 | Abb. 9.13 a) Nephroide als Hüllkurve aus Kreisen, b) Nephroide als Hüllkurve von Kreisen, die alle die y-Achse berühren, Mittelpunkt Qk auf einem Ursprungskreis mit Radius a, c) Nephroide als gespitzte Epitrochoide (Epizykloide) mit Rastkreisradius a, Rollkreisradius a/2 | |
| a) im GeoGebra-Book
a) download
b) und c) im GeoGebra-Book b) und c) download
| |||
| Kap: Seite 9.4.2.2: S. 281 |
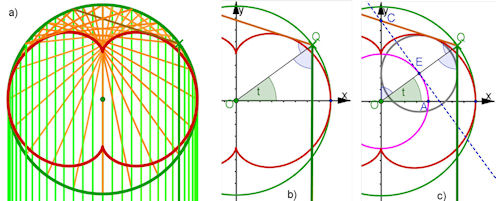 | Abb. 9.14 a) Nephroide als Katakaustik, Reflexion an einem Kreis mit Radius 2a, b) Konstruktion der Reflexion parallelen Lichtes, c) Beweisfigur: die Reflexion passt zur Hüllkurven- Konstruktion aus Abb. 9.13 b) | |
| a) im GeoGebra-Book
a) download b) und c) im GeoGebra-Book
b) und c) download
| |||
| Kap: Seite 9.4.2:4 S. 283 |
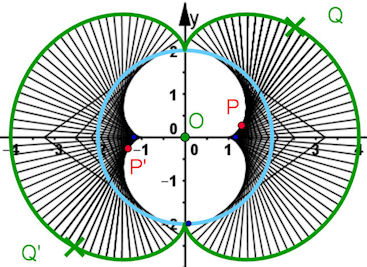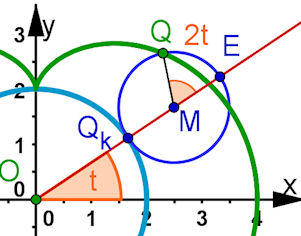  | Abb. 9.15 Evolute der Nephroide
Aufgabe 9.8: Konstruieren Sie die Normalenschar (siehe 9.3.2). Die Evolute ist eine um 90° gedrehte, auf die Hälfte verkleinerte Nephroide. Realisieren Sie handwerklich, dass der Berührpunkt P die Mitte zwischen Q und dem einen Schnittpunkt der Normalen mit dem (hellblauen) Grundkreis ist. Im Bild sind die Normalen nur bis zur x-Achse gezeichnet und die untere Hälfte ist durch Punktspiegelung am Ursprung erzeugt. im GeoGebra-Book
download
Aufgabe 9.8 Nephroide und ihre EvoluteBedeutung des Parameters t in der waagerechten Lage der Ausgangs-Nephroide
Mathematica-Notebook für Aufgabe 9.8
Das Mathematica-Notebook zum Lesen
| |
 |
Die Mitten der Strecken $QB$ liegen auf der Evolute
Unabhängige Bestätigung
Dazu weiteres in Aufgabe 9.11.
Mathematica-Notebook für Aufgabe 9.8
Das Mathematica-Notebook zum Lesen
| ||
| Kap: Seite 9.4.2.4: S. 283 Zusatz |
 | Zusatz: Das Tangentenquartett in Aufgabe 9.8 Nephroide und ihre Evolute (unten)
Tangentenquartett download
| |
| Kap: Seite 9.4.3: S. 282 9.9 |
 |
Aufgabe 9.9 Die Nephroide und ihre Pedalkurven
download
Mathematica-Notebook
Das Mathematica-Notebook zum Lesen
| |
| Kap: Seite 9.4.2.4: S. 283 9.10 |
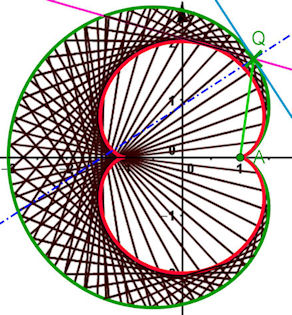
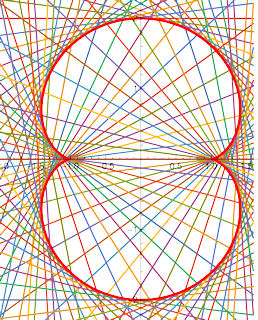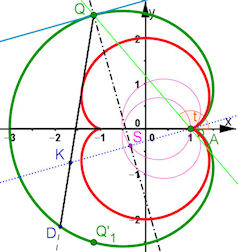  | Abb. 9.16 Eine Kaustik der Kardioide ist die Nephroide
Aufgabe 9.10: Zeichnen Sie eine Kardioide als Parameterkurve nach Gleichung 9.16 ohne das +a. Konstruieren Sie zu einem zugfesten Punkt Q Tangente und Normale. Das Bild der Geraden AQ bei Spiegelung an der Normalen ist der reflektierte Strahl. Auf ihm definieren Sie eine Strecke, deren Spur die Nephroide zum Vorschein bringt. Raten Sie die Nephroidengleichung und prüfen Sie durch Einzeichnen. Wenn Sie mögen, leiten Sie die Gleichung her. Die unteren Strecken erhält man durch Spiegeln der oberen an der x-Achse. Aufgabe 9.10 Die Nephroide als Katakaustik der Kardioide
Übriges: Kaustik heißt Brennlinie. Wenn diese durch Reflexion entsteht, heißt sie Katakaustik Wenn diese durch Brechung entsteht, heißt sie Diakaustik Datei für das obere BildDie Beweis-Konstruktion
Mathematica-Notebook
Das Mathematica-Notebook zum Lesen
Die Idee für einen rechnerischen Beweis ist folgende: Zu Q auf der Kardioide werden die Tangentensteigung und die Gleichung der Normalen, die als Einfallslot dient, bestimmt. Das Lot von A auf die Normale hat den Fußpunkt S, die Spiegelung von A an S liefert K. Die Schar der Geraden QK, oder Ausschnitte davon, erzeugen als Hüllkurve die Nephroide. | |
| Kap: Seite 9.4.2.4: S. 283 9.11 |
 | Aufgabe 9.11 Nephroide und Analysis
Mathematica-Notebook
Das Mathematica-Notebook zum Lesen
| |
|
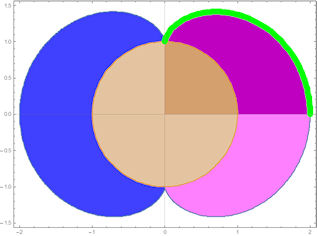| Betrachtungen zu der rechten Seite finden sich in Aufgabe 9.11 Nephroide und Analysis und
Mathematica-Notebook
Das Mathematica-Notebook zum Lesen
Die Mitteneigenschaftet ist in Aufgabe 9.8 Nephroide und ihre Evolute (unten) bewiesen. Mitten und andere Abstände
| ||
| 9.5 Inversion am Kreis | |||
| Kap: Seite 9.5.1.1: S. 285 |
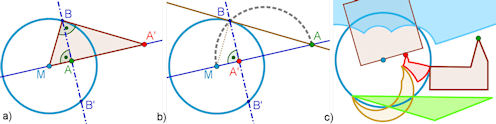 | Abb. 9.17 Kreisspiegelung = Inversion am Kreis mit dem Mittelpunkt M und dem Radius
k. Vorschlag: Mit Bild c) und dem Blackbox-Whitebox-Verfahren die Inversion erkunden.
| |
| Bild a) Abbildung eines Punktes A im Innern des Inversionskreises: Senkrechte auf MA,
in einem Schnittpunkt mit dem Kreis Tangente als Senkrechte auf dem Radius, Schnittpunkt
von Tangente und MA ist der Bildpunkt A'.
Bild b) Umgekehrt: Abbildung eines Punktes A auserhalb des Inversionskreises: Thaleskreis auf Strecke MA, im Schnittpunkt Lot auf MA fällen, der Lotfußpunkt ist der Bildpunkt A'. Bild c) Mit dem Button "Kreisspiegelung" werden Polygone (Kirche, Quadrat, Dreieck) am blauen Kreis gespiegelt. | |||
| Kap: Seite 9.5.1.4: S. 287 |
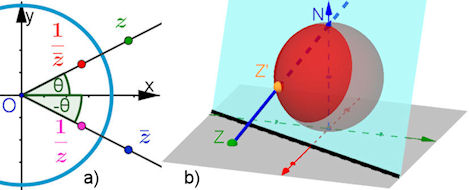 | Abb. 9.18 Inversion komplex: a) die komplexe Zahl z, ihre konjugiert komplexe Zahl ¯z und beide algebraisch Inversen, ihre Kehrwerte. Die Punkte auf einem Strahl sind geometrisch invers. b) Die Gauß’sche Zahlenebene wird eineindeutig auf die Riemann’sche Zahlenkugel abgebildet. im GeoGebra-Book
download
| |
| Kap: Seite 9.5.2: S. 288 |
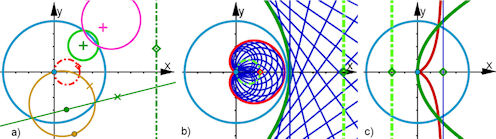 | Abb. 9.19 Inversion von Kurven an einem Kreis vom Radius k um den Ursprung O. Die Beweise
folgen im Text, für b) und c) in Abschnitt 9.5.2.3.
a) im GeoGebra-Book
a) download
b)im GeoGebra-Book
b) download c) im GeoGebra-Book
c) download | |
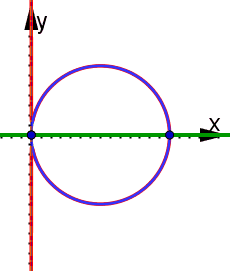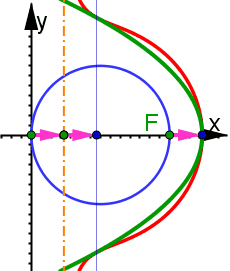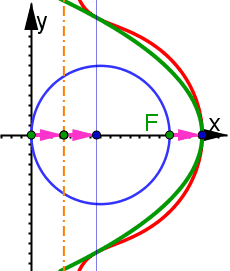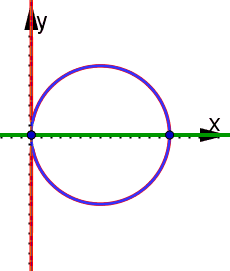
| Bild a) Eine Parallele zur y-Achse (grün strichpunkt) durch A = (a, 0) wird abgebildet auf einen
zu OA symmetrischen Kreis (rot strichpunkt) durch O und ( k^2/a , 0). Eine beliebige Gerade (grün)
wird auf einen Kreis (ockerfarben) durch O abgebildet. Ein beliebiger Kreis (hellgrün) wird auf
einen Kreis (violett) abgebildet, wobei das Bild (+ violett) seines Mittelpunkts (+ grün) nicht
Mittelpunkt des Bildkreises wird.
Bild b) Durch eine Leitgerade (hellgrün gestrichelt) und einen Brennpunkt im Ursprung wird die grüne Parabel definiert. Ihr Inversionsbild ist eine Kardioide mit ihrer Spitze im Ursprung. Die blauen Tangenten an die Parabel haben als Bilder Kreise durch den Ursprung, die die Kardioide von innen berühren. Bild c) Durch die Leitgerade und den Ursprung wird zunächst der Brennpunkt durch Punktspiegelung und dann die grüne Parabel definiert. Ihr Bild (rot) ist die Cissoide des Diokles mit der Asymptote (blau). Unten zeigt sich, dass diese nicht immer durch den Brennpunkt der Parabel verläuft. | |||
| Kap: Seite 9.5.4.1: S. 292 |
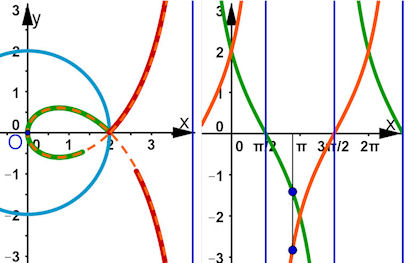 | Abb. 9.20 Inversion der Strophoide ergibt
dieselbe Strophoide, wenn ihr Scheitel im
Ursprung und ihr Doppelpunkt auf dem
Inversionskreis liegt. Man sagt, die Strophoide
ist an-allagmatisch. Das Bildpaar
links zeigt, wie schon oft in diesem Buch, die
gekoppelte polar-kartesische Darstellung. Die
grüne Urbild-Strophoide ist nur bis thtea = 2.8
gezeichnet, das gilt dann auch für ihr rotes
Bild. Orangefarben gestrichelt ist die gesamte
Bild-Strophoide.
| |
| Kap: Seite 9.5.5: S. 293 9.12 |
 im GeoGebra-Book
download | Aufgabe 9.12 Inversion der Kegelschnitte in Scheitellage
Mathematica-Notebook gemeinsame Datei für Aufg. 12, 13 und 14
Das Mathematica-Notebook zum Lesen
| |
| Kap: Seite 9.5.5: S. 293 9.13 |
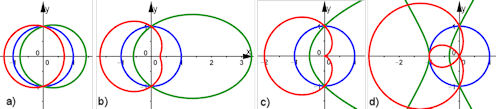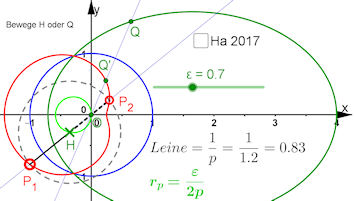  | Aufgabe 9.13 Inversion der Kegelschnitte in Brennpunktlage
Oberes im GeoGebra-Book
download
Mit Bezug zur Konstruktion der Pascalschen Schnecken download
Mathematica-Notebook gemeinsame Datei für Aufg. 12, 13 und 14
Das Mathematica-Notebook zum Lesen
| |
| Kap: Seite 9.5.5: S. 293 9.14 |
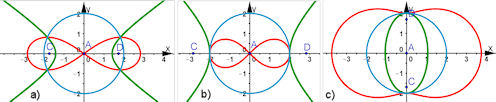 | Aufgabe 9.14 Inversion der Kegelschnitte in Mittelpunktslage
im GeoGebra-Book
download
Mathematica-Notebook, gemeinsame Datei für Aufg. 12, 13 und 14
Das Mathematica-Notebook zum Lesen
| |
| Kap: Seite 9.5.5: S. 294 9.15 |
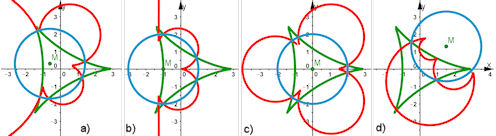 | Aufgabe 9.15 Inversion der Steiner-Kurve
im GeoGebra-Book
download
Mathematica-Notebook, Herleitung der immplziten Gleichung
Das Mathematica-Notebook dazu zum Lesen
Mathematica-Notebook, Lösung Afg. 9.15
Das Mathematica-Notebook dazu zum Lesen
| |
| Kap: Seite 9.5.6: S. 294 |
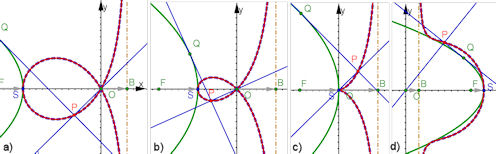
 | Abb. 9.21 Inversion von evt. anallagmatischen Kurven a) Die Steiner-Kurve und eines ihrer Inversionsbilder, s. Aufgabe 9.15, b) und c) Cassini’sche Kurven invertiert, s. Aufgabe 9.16, d)Königin der Spiralen invertiert, s. Aufgabe 9.17 | |
| a) im GeoGebra-Book
a) download siehe auch Afg. 9.15.
b) und c)im GeoGebra-Book
b) download
c) download siehe auch Afg. 9.16
d) im GeoGebra-Book
d) download siehe auch Afg. 9.17
| |||
| Kap: Seite 9.5.6.2: S. 295 9.16 |
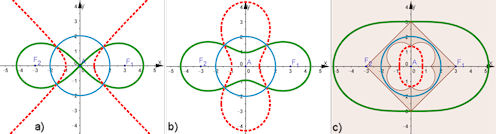
| Aufgabe 9.16 Cassini'sche Kurven und ihre Inversion
im GeoGebra-Book
download
| |
 |
Mathematica-Notebook
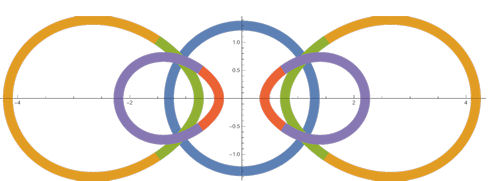Das Mathematica-Notebook zum Lesen
| ||
| Kap: Seite 9.5.6.2: S. 295 9.17 |
 |
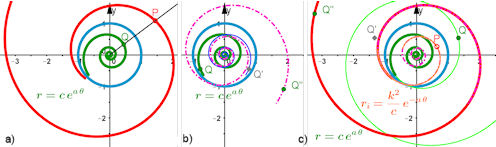Aufgabe 9.17 Königin der Spiralen und ihre Inversion
im GeoGebra-Book
download
| |
| 9.6 Exoten-Kurven | |||
| Kap: Seite 9.6.1: S. 296 |
 | Verbale Aufgabe S. 296 f zur konstanten Krümmung | |
| Kap: Seite 9.6.2: S. 297 |
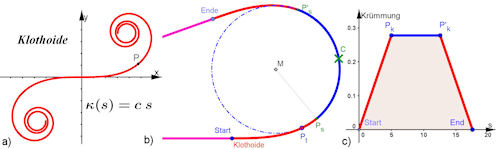 | Abb. 9.22 Keine Straße ohne Klothoide a) „ganze“ Kurve, b) Fahrbahn: Gerade, Klothoide, Kreis, Klothoide, Gerade, c) Krümmungsverlauf a) im GeoGebra-Book a) download
b) und c) im GeoGebra-Book b) und c) download
| |
| Zusatz | 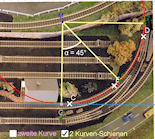 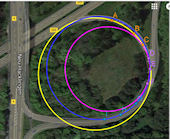 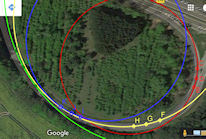 Klothoide, Modell-Eisenbahn, reale Trassen  In drei Vorträgen verwendet: Sience Slam (Leuphana Universität, Nov. 2016) Klothoide und andere Anwendungen von Kurven (MNU Brmerhaven Nov. 2017) Keine Stroße ohne Klothoide, (GDM und DMV Paderborn März 2018) | ||
| Kap: Seite 9.6.3: S. 299 |
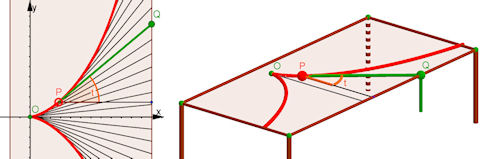 | Abb. 9.23 Traktrix, der Weg der Uhr an der Kette Man stelle sich vor, eine Taschenuhr P werde mit einer Kette der Länge k an einer Tischkante entlang gezogen. Beim Start ist die Kette senkrecht zur Tischkante. Die Uhr P bewegt sich dann auf einer Kurve, die in jedem Moment die Richtung der Uhrkette als Tangente hat. im GeoGebra-Book
download
| |
| Kap: Seite 9.6.4.1: S. 300 |
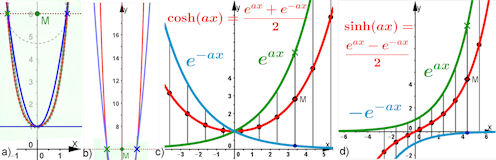 | Abb. 9.24 Hyperbolicus-Funktionen
a) und b) Kettenlinie: Über das Foto einer hängenden Kette ist in Rot die Kettenlinie gelegt und in Blau zum Vergleich eine Parabel angezeigt, c) und d) Kosinus- und Sinus hyperbolicus Funktionen sind als Mittenkurven elementarer e-Funktionen dargestellt. a) und b) im GeoGebra-Book
a) und b) download
Berechnungen dazu ausführlich in Aufgabe 9.18 Punkt 4. | |
| Kap: Seite 9.6.4.4: S. 303 |
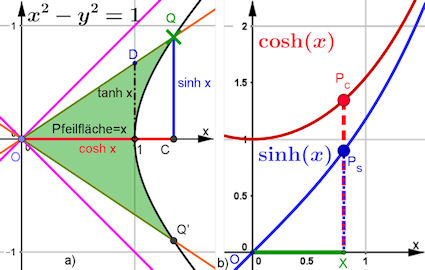 | Abb. 9.25 Die Areafunktionen
liefern tatsächlich
Flächen. Aus
sinh(x) = 0.85
folgt mit dem Areasinus
x = arsinh(0.85) = 0.77
und das ist die Größe der
pfeilförmigen (grünen)
Fläche, ein Areal. Ebenso folgt aus cosh(x) = 1.3 nun mit dem Areakosinus x = arcosh(1.3) = 0.77. Die gekoppelten Grafikfenster zeigen die Zusammenhänge. im GeoGebra-Book
downloadVerbreitet herrscht Unkenntnis und die Funktionen werden ArcusKosinusHyperbolicus u.s.w. genannt. Z.B. in Mathematica heißt es ArcCosh[...]. Darum hier die entsprechende Seite aus dem Buch
und die zugehörige Mathematica-Datei Area hyperbolicus Mathematica-Notebook und < target="_blank" a href="areahyperbolicus.pdf">
Das Mathematica-Notebook zum Lesen | |
| Kap: Seite 9.6.4: S. 305 9.18 Punkte 1. und 2. |
 |
Aufgabe 9.18 Kettenlinie
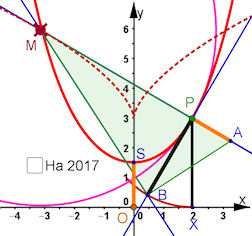Diese Aufgabe hat mehrere Teile, die in der pdf-Datei gemeinsam behandelt sind. Die Bilder und zugehörige Dateien folgen hier einzeln.
| |
| 9.18 Punkte 3. und 4. | 
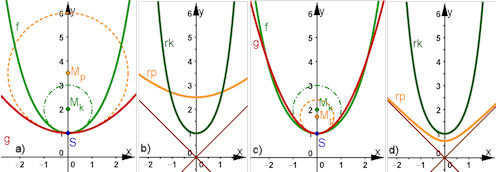
| Parabel und Kettenlinie inAufgabe 9.18 Kettenlinie download weite Form der Parabel download enge Form der Parabel | |
| 9.18 Punkt 5. | 
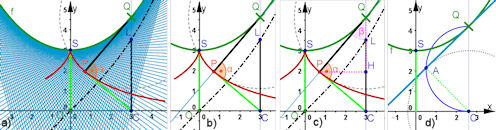
| Kettenlinie, ihre Evolvente, Taktrix und deren Evolute inAufgabe 9.18 Kettenlinie | |
| Kap: Seite 9.6.4.5: S. 306 |
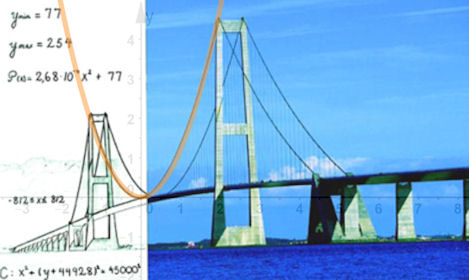 | Abb. 9.26 Die Storebælt-Brücke (Dänemark) auf
einem Plakat zum „Word Mathematical
Year 2000“, die in GeoGebra erzeugte
gelbe Parabel ist von mir hinzugefügt.
Wie die Beschriftung deutlich macht,
haben nämlich Seile, die (Linien-)Lasten
tragen, nicht die Form einer Kettenlinie,
sondern die Parabelform ist angemessen.
| |
Quelle: DMV-Website 2000, http://www.mathematik.de/mde/information/wasistmathematik/wasistmathematik.html Thomas Perters http://www.mathe-seiten.de/kettenlinie.pdf, Bweise für Kettenlinie, aber auch für Parabel bei Linieanlast. Bild: © Vagn Lundsgaard Hansen | |||
| Kap: Seite 9.6.4.5: S. 306 Afg. 9.18 |
 | Abb. 9.27 Rotationskörper, die x-Achse weist nach oben. a) Hyperboloid, b) Paraboloid, c) Katenoid, die Minimalfläche, sie wird von einer Seifenhaut zwischen den zwei Kreisen gebildet. In der nachfolgenden Mathematica-Datei sind auch diese 3D-Bilder erzeugt. | |
| Kap: Seite 9.6.4.5: S. 308 9.19 |
download
Mathematica-Notebook
Das Mathematica-Notebook zum Lesen | Aufgabe 9.19 Katenoid als Minimalfläche
| |
 Prof. Dr. Dörte Haftendorn |
Erstellt August 2016, Update |
www.kurven-erkunden-und-verstehen.de |
| ||
